今天無聊,做起CSC3270四道數據結構習作。
PKU1182 食物链
依據路徑壓縮,可以對x-->y帶三種標號﹕ label(x) = 0 (x 與 y 同類), 1 (x 吃 y), 2 (y 吃 x)。
計算路徑計縮時必須先取x的根點, rx。 對於find(x)一遍後,最多只有這種結構﹕x-->y-->rx。假設它是合法的,那麼label(x)的更新必然是(label(x) + label(y))%3 (可用簡單向量理解),然後對x進行路徑壓縮。
要判斷x y的關係,先尋找它們的根rx及ry。如果rx == ry,可以直接判同類(label(x) = label(y))或者x吃y ((label(x) - label(y) + 3) % 3 == 1 及 x != y)。
若rx != ry 顯然不會有矛盾。這意味著可以通過并合兩者來構造新的樹。對於x-->rx-->ry<--y,若果認為x跟y是同類的話,必有label(x) + label(rx) = 0 + label(y)。若果認為x吃y的話則有label(x) + label(rx) = 1 + label(y)。繼乎直接更新label和進行普通union就成。
PKU2481 Cows
如果任何可以強於[Si, Ei]的牛[Sj, Ej],必須有Sj <= Si和 Ei <= Ej。可以想到當我們從最大的E值開始,相同E值的依最小S值來處理線段的話,保証處理當前線段時,所有強於它的線段都已經處理過了(並且不強於它的線段沒有被處理過)。此刻強於線段i的已處理線段必然都有<=Si的值。因此我們可以憑已處理並少於等於Si的S值進行統計並計算答案。然後把Si加進表中。這裡我們直接使用樹狀數組。對於重覆的[S, E]值,我們直接用上一個處理線段的值,因兩者有相等答案。緊記亦需把它加進數組中。
PKU2777 Count Color
純粹普通線段樹應用。一種顏色可用一個位元來記著。
PKU1442 Black Box
用最大堆及最小堆。每次把新的數放進最大堆。只要當前最大堆的大小超過counter,便把它放到最小堆內。最大堆永遠保持首counter小的數。最小堆的最小值便是答案,記得把它放會最大堆中。
2010年5月21日 星期五
2010年5月19日 星期三
ZOJ3334 Body Check
ZOJ 5月月賽題目。
大意是給了n個實數,代表了n個人需要完成身體檢的時間。有m個醫生為他們作身體檢查。一個人可以分開不同時段給不同醫生作身體檢查,唯獨是一個人不可以同一時間給多於一個醫生作身體檢查。另,醫院時刻也只能有這兩個情況﹕要麼m個醫生都在為不同的人作身體檢查,要麼就只有一個人在加班。問,最少需要多久能為所有人完成檢查?
首先,可以通過安排,使得工模式為「m位醫生工作 --> 一醫生工作」。如果一個人不可以分開時段給不同醫生檢查,可以得出問題的一種特例就是partition問題,是NP-Complete的。正因為可以任意分開時段,我們第一個想法就是直接取平均數。不過需要注意另一個限制「一個人不可以同一時間給多於一個醫生作身體檢查」。因為像5和5.1而m=2的話,雖然平均數是5.05,但是第二個人的0.1無法分拆成兩個不同時段。可以直接觀察得出,假若有一個需時大於平均數的話,剩出來的時間基本上無法放到任何平均數線之前,因為這位人本身已經獨佔了平均數線以前的時段。若然沒有這樣的問題的話,那麼我們必定可以安排所有人在平數時限前完成檢查。基於平均數本是最優的,所以我conjecture了這個算法﹕
為所有數取平均數,然後檢查每個數,若大於平均數,把多出的加到答案裡,然後把它們設為平均數,完成後重新再取平均數檢查;否則把平均數加到答案裡,並輸出答案。
一次AC。
2009年12月23日 星期三
ZOJ 3282 Go Downstairs
ZOJ 12月月賽題目。
給出每行有及僅有一個梯級,有或沒有金幣,幣值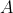 。每一行的梯級必然在上一行的梯級的左方或右方。一個在這張圖上的遊戲是這樣的﹕首玩者可以以費用
。每一行的梯級必然在上一行的梯級的左方或右方。一個在這張圖上的遊戲是這樣的﹕首玩者可以以費用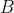 選擇移去該行的梯級,麼次玩者會垂直掉到最接近的梯級,或離開地圖。如果該梯級有金幣的話也一併移掉。次玩者可以選擇修復剛移除的梯級(最多只能操作
選擇移去該行的梯級,麼次玩者會垂直掉到最接近的梯級,或離開地圖。如果該梯級有金幣的話也一併移掉。次玩者可以選擇修復剛移除的梯級(最多只能操作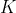 次),但不能修復原有的金幣。每當他走到有金幣的話他必定會取走。次玩者必然從最頂層出發。首玩者先操作。當次玩者跳離地圖,遊戲便結束。
次),但不能修復原有的金幣。每當他走到有金幣的話他必定會取走。次玩者必然從最頂層出發。首玩者先操作。當次玩者跳離地圖,遊戲便結束。
問,若果金幣全屬首玩家所有,那麼在雙方採取最優策略底下,首玩家的損失最小是甚麼。
首先,不難留意這張圖可以化為有向無環圖。頂層梯級為出發點,並構造虛擬終點(即跳離地圖的狀態)。然後可以結論這道題目是Minimax題。簡單的動態規劃可以搞定。狀態為 ,當中
,當中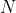 是行數、
是行數、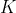 是用了多少次修復,
是用了多少次修復,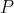 為玩者編號。轉移方程也很一般,不贅述。
為玩者編號。轉移方程也很一般,不贅述。
此題唯一比較不足的地方是,應該容許兩層梯級可以共處同一垂直位置,而且應該考慮同一梯級可以重覆修復及移除。但是題目實際上如果移除了,某人就必須走下一級。這樣,下列的情況會得出不一樣的答案﹕
5 5 5 1 2
G....
G....
G....
G....
G....
(注意根據原題描述,此情況絕不會發生)
給出每行有及僅有一個梯級,有或沒有金幣,幣值
問,若果金幣全屬首玩家所有,那麼在雙方採取最優策略底下,首玩家的損失最小是甚麼。
首先,不難留意這張圖可以化為有向無環圖。頂層梯級為出發點,並構造虛擬終點(即跳離地圖的狀態)。然後可以結論這道題目是Minimax題。簡單的動態規劃可以搞定。狀態為
此題唯一比較不足的地方是,應該容許兩層梯級可以共處同一垂直位置,而且應該考慮同一梯級可以重覆修復及移除。但是題目實際上如果移除了,某人就必須走下一級。這樣,下列的情況會得出不一樣的答案﹕
5 5 5 1 2
G....
G....
G....
G....
G....
(注意根據原題描述,此情況絕不會發生)
2009年9月28日 星期一
Lucas Theorem
讀過組合或概率的朋友都知道從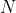 種互不相同的東西取
種互不相同的東西取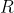 種,有
種,有 種不同的組合,或記作
種不同的組合,或記作 。此式可以寫成以下形式﹕
。此式可以寫成以下形式﹕

如果給出一個質數 ,問
,問 除
除 的餘數是多少?
的餘數是多少?
1878年Lucas提出以下定理﹕

當中
 和
和

就是把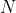 和
和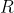 寫成
寫成 進制,然後每一個位的對應系數求相同問題,再取積則成。
進制,然後每一個位的對應系數求相同問題,再取積則成。
把這個問題的轉化有一個好處,就是當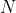 非常大的時候,而
非常大的時候,而 相對地小,利用Lucas定理運算同樣問題會快很多。剩下的問題就是求
相對地小,利用Lucas定理運算同樣問題會快很多。剩下的問題就是求 除
除 的餘數是多少。把此式展開,
的餘數是多少。把此式展開,

根據模運算,可以計算每分數除 的餘數,然後取積除
的餘數,然後取積除 的餘數即可。
的餘數即可。
問題是,模運算對 除
除 的餘數不能直接用分子分母的方法取得。其中一個方法是用擴張輾轉相除法,另一個方法比較巧妙。因為
的餘數不能直接用分子分母的方法取得。其中一個方法是用擴張輾轉相除法,另一個方法比較巧妙。因為 是質數,根據費馬小定理,若
是質數,根據費馬小定理,若 與
與 互質,可得以下公式﹕
互質,可得以下公式﹕

利用模運算,可得﹕


當中
求 除
除 的餘數直接等價於求
的餘數直接等價於求 除
除 的餘數。求
的餘數。求 可以利上式以
可以利上式以 時間求出。
時間求出。
由於 ,此問題可以在
,此問題可以在 時間內求出。
時間內求出。
延伸﹕因為對於任何系數 和
和 ,都必然小於
,都必然小於 。所以當
。所以當 為質數,費馬小定理必然成立。如果當
為質數,費馬小定理必然成立。如果當 呢?我們可以直接取其餘數,再套入費馬小定理即可。注意當餘數等於
呢?我們可以直接取其餘數,再套入費馬小定理即可。注意當餘數等於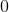 表示
表示 不存在。
不存在。
如果給出一個質數
1878年Lucas提出以下定理﹕
當中
就是把
把這個問題的轉化有一個好處,就是當
根據模運算,可以計算每分數除
問題是,模運算對
利用模運算,可得﹕
當中
求
由於
延伸﹕因為對於任何系數
訂閱:
文章 (Atom)
