Lucas Theorem

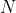
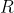
讀過組合或概率的朋友都知道從種互不相同的東西取種，有種不同的組合，或記作。此式可以寫成以下形式﹕

如果給出一個質數，問除的餘數是多少？


1878年Lucas提出以下定理﹕

當中
和

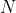
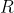
就是把和寫成進制，然後每一個位的對應系數求相同問題，再取積則成。
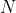
把這個問題的轉化有一個好處，就是當非常大的時候，而相對地小，利用Lucas定理運算同樣問題會快很多。剩下的問題就是求除的餘數是多少。把此式展開，

根據模運算，可以計算每分數除的餘數，然後取積除的餘數即可。
問題是，模運算對除的餘數不能直接用分子分母的方法取得。其中一個方法是用擴張輾轉相除法，另一個方法比較巧妙。因為是質數，根據費馬小定理，若與互質，可得以下公式﹕

利用模運算，可得﹕


當中
求除的餘數直接等價於求除的餘數。求可以利上式以時間求出。
由於 ，此問題可以在時間內求出。

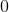
延伸﹕因為對於任何系數和，都必然小於。所以當為質數，費馬小定理必然成立。如果當呢？我們可以直接取其餘數，再套入費馬小定理即可。注意當餘數等於表示不存在。