Codeforces #7 D Palindrome Degree

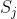
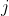
題意﹕給了一字串，長度為。設為一長度的前綴。我們把一個長度為的字串說是-迴文，若以下條件成立﹕
1) 是一個迴文；
2) 的前綴和後綴皆是-迴文。根據定義，任意字串(包括空字串)皆為0-迴文。

現在設若且僅若是一個-迴文。題目要求。

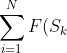未進入解之前，首先需要了解一件事。

引理 1﹕對於任何長度為的字串，若是迴文，是-迴文的話，那麼的長度為的後綴也是-迴文，並且和相同。

証明 1：設為字串的逆字串。假設的長度為的前後綴分別為和。設，。那麼。因為，。因此有和。若是-迴文，則本來。因此，即也是-迴文。


因此，我們算的時候可以用動態規劃﹕



那麼，答案是求所有前綴迴文，並以上述轉移方程算出陣列和即可。
問題是﹕如何有效地求所有前綴迴文？

想了幾天，實在沒有頭緒。如果直接算最長前綴迴文的話就很簡單的，只需利用失敗函數和字串即可。可是它卻不似包含了所有前綴迴文的資訊。因此，放棄了，找到幾個日本人寫的blog，發現他們用了一個算法，叫Manacher Algorithm。它的目的是求出最長前綴迴文的中點，但計算過程則計算了所有以某字元可延伸的最長迴文長度。那麼此算法則包括找出所有前綴迴文，當然，也可以用來找最長前綴迴文。先介紹此算法。

Manacher算法
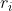
對於長度為的字串，定義為最大整數使得即以第字元為單位的最長可延伸成迴文的半徑。Manacher給了以下定理﹕

定理 2: 對於，則有

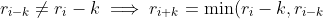1. 和
   
2. 。
   

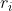
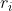
証明 2: 先証明1)。因為第字元半徑為，當中第字串的半徑是。若果不超過的話，表示第字元的最長可延伸迴文被第字元的包含了，則用類似定理 1可以得出(即)。否則的話，假設，那麼第字元的最長可延伸迴文超越了第字元的。但基於類似定理 1(我們可以把定義為任意迴文)，第字元可以再延伸，則不是最長的，因此有矛盾。所以(最不突破界限的半徑作為其半徑)。
對於2)，則可以基於1)的去思考。但第字元的半徑則卻可以突破第字元的半徑。考慮以下字串﹕

01abbaccabbac

   |  i  |

   x     y

現在設。可以看到但。

那麼，利用定理 2計算所有字元的半徑會否很高效？首先，留意到對於第字元，任何第位經1)去更新數值的時候，已經不用重覆計算。唯一的情況則是2)發生，而且枚舉的時候，2)只會發生在1)之後。因此，當枚舉至的時候2)發生了，則跟據定理 2所示，立即跳至第位計算其半徑。因為定理說明，因此找出可直接從算起。因此可知的跳躍是隨的增加而加快的。算法被証明是的。我沒有很小心的去証明，但可以聯想的是少的話，雖然增長很慢(每次移很少)但半徑都很少，因此每次迭代都很快完；相反很大的話，我們很快就可以以一次送代算出大部分並且大幅前躍，感覺也很快會完成。

至於編寫的時候，留意上述是適用於偶數長度半徑，但奇數長度半徑又怎樣算出來呢？這裡的方法是插入dummy點來計算半徑，但每個字元會被多算一次。這方法亦可看作迭代的時候移動半步，而枚舉其半徑時也以半步為單位移動。

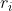
計算了之後可以簡單地找出前綴迴文的末點，然後應用最被初的轉移方程計算答案。