Codeforces #51 D Geometrical Problem

題意﹕給了個整數的數組，問其本身是否幾何數列？若否，問能否經移除一個元素使得餘下的數列成為幾何數列？假設。

首先，檢測是否幾何數列不難，線性時間就能做到了，另需要特別留意首項為0的情況。但能否高效的做到檢測移除單項成為幾何數列就不簡單。直觀做法是逐一移除，再檢測是否幾何數列，但對於這數據範圍，顯然有點慢。

但，可能的數列等比只有3個(這裡不考慮首項為0的情況，可特別處理)﹕。第三個等比表示移除第二項，第二個等比表示移除首項，至於第一個等比，表示被移除的項在是第3至第N個其中一個。後兩個情況可以再應用一次線性時間的檢測，但第一個情況可以經對比有多少個餘項不符合等比數值即可。若不符合數至少有2，則表示移除第3至第N項其中之一都不能讓數列成為幾何數列。因此本題能以時間內解決。

Codeforces #6 E Exposition

題意﹕給了長度為的數列，取一連續子序列使得其最大和最小元素相差最多為。問該長度最長為多少？並且輸出所有符合條件的連續子序列的長度起點和終點。

很經典的RMQ，可以用Sparse Table或線段樹完成。維護兩棵線段樹，一記區間的最大值，一記區間的最小值。有一個簡單的觀察。

觀察: 對於固定的，是一單調上升序列，是一單調下降序列。因此是一單調上升序列。

由此可以，枚舉，然後可以用二分法，二分長度，找出最長的長度使得。
最長長度則是。

在線段樹查詢區間是，而枚舉加二分長度，整個算法是。

SRM 498 DIV 1 Easy + Medium

今次srm miss了，不過Easy和Medium是想不到的容易。也好，最近的srm題越來越難，這些題目應該多出點，有時考核選手的編碼能力和速度也是很重要的。期待以後srm也會多出點這類題目。

Easy
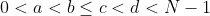
題意﹕要求檢查給定的數列是否符合A[0]~A[a], A[c]~A[d]都是正差等差數列，A[a]~A[b], A[d]~A[N-1]是負差等差數列，A[b]~A[c]元素都是相等，其中。枚舉即可。注意檢查邊界﹕a取值1~N-2，b取值a+a~N-2，c取值b~N-1，d取值c+1~N-2。

Medium
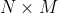
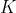
題意﹕給了一個的格子，每個格子都有不同顏色的石子。現在給了個不同的著色的格子，問有多少個不同的石子排列，使得新的排列中，每個石子與著色的格子距離與其原來排列的一致。距離函數是。

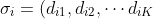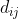
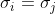
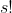
問題可以看成是pSort的變種。定義某石子的距離特徵為，當中為第i石子與第j個著子格子的距離。不同的石子i, j屬於相同的交換群，若且僅若。因此，對於群組大小為的則有的排列與原來的一致。因此只需把所有不同的群組的排列數取積即可。我則用map<vi, int>來記錄交換群的數量，有點無恥，也有點暴力，但也過了。

Practise room得688分，實際比賽應該打了7折左右，排名可以在31至249之間，可見速度與準繩度有多重要…

Codeforces #60 C Mushroom Strife

題意﹕給了一個點邊的圖，每點賦一個數值，每條邊給了，分別代表了。現在只給了每條邊上的，問是否能找到滿足這些邊上的數值的條件。若存在解則輸出任意一組答案。保証。

比賽寫了一些錯的東西，因為最初以為正確的做法會很慢………

首先，在每一個連通子圖任意選一點，然後任選一條連接的邊，先求因式分解。而也必然是。因此有取值，而且。因此選定後這連通子圖的其他點的值則可以經DFS用求得。

注意DFS時須要檢查取值是否正確的﹕若在一點為一未經過的點賦值，則必需檢查。若已賦值則需檢查且。

整個算法時間複雜度是。

另，注意檢查時小心溢出，即，需要用到64位整數。