本題是POJ八月份的月賽題
大意是給出一個半徑為10的圓,求切了
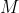
刀之後所有形狀的最大表面積。
一刀可以從兩個弧度判定。保証不會存在至少三刀相交同一點的情況。
可以留意到的是此圖包含所有相交點及線後可以轉化成一個Planar Graph。
而且任意頂點最多只Degree 4。構建平面圖的方法可以這樣想﹕先從圓弧上的交點以極角排序,然後環狀地每兩點加上一條邊,並標註其為弧。對於其他直線,先取一刀

,然後從所有切法

求出所有相交點。我們可以知道

上所有線段代表的頂點與邊。然後按x, y排序,連續兩點必對應平面圖上的一條邊。
利下來的是求枚舉所有可能形狀。意兩件事實﹕
(1) 弧只能屬於一個形狀。
(2) 直線必定屬於兩個形狀。如果限定形狀的traversal必須逆時針,那麼對於一條無向邊

,其有向邊

及

各屬於一個不同的形狀。
因此如果以每一點每一條邊traversal,若得出某
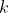
邊形狀
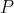
,則
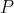
必然被traverse
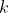
遍。從上述事實,每條邊只會traverse一次,故可為每一條邊加上visited限制重覆枚舉。假設我們枚舉邊

,則下一條應該traverse的邊應該是從

逆時針轉角最大的,設該邊為

。先從簡單的情況討論,如果沒平面圖不含弧,找出

的一個簡單方法是﹕把從
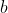
相鄰的點按極角排序,

應該是

之前。所以從

出發,找出

,只需搜尋按排序的邊直至遇上

,那麼環狀地上一條邊便是

。
如果從直線

出發,有可能會遇上chord。(即

的下一條邊是

),所以按極角排序的點若在圓弧上,對於直線和弧的

,優先次序應先給予弧。
剩下來的是從弧

出發的情況。由於事實(1)的關係,圖上不存在弧

。找尋下一條邊的法則會與直線的不太一樣。但由於圓弧與排序的特殊關係,弧

與應該是被夾在圓上下一條弧

和應該traverse的下一條邊

中間。所以只需遇上弧

,環狀地上一條直線便是

。簡單問題﹕為甚麼弧一定轉向直線?
記得留意,如果遍歷時遇上弧,必須先為面加上chord面積。設

為半徑,

是弧上兩點,其夾角為
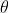
,則有如下兩個公式計算chord面積﹕
(1)

(2)


沒有留言:
張貼留言