比賽題目較為簡單,但是仍然表現得不夠好。
A: 問給了4個互相不同的數
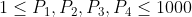
,給了範圍

,問當中有多少個數,使得在至少7種

的不同排列中,該數在取模的順序下仍然保持不變。看了之後都不用懷疑,直接就

暴搞了。但留意一下取模順序本來就是符合交換性的,即
\bmod{b}=(x\bmod{b})\bmod{a})
,因此只需對一種排列(例如輸入中的排列)下試了所有數看看是否在取模順序下不變即可。省卻了24!的排列。
然而,本題有
)
的算法。假設

,可知保持取模下不變的數只能在

,即,其餘取模是多餘的。因此答案即是
-a+1))
。
B: 給定

個整數

,定義操作
, i\ne j, 0 \le k \le 99, x \in \mathbb{R}, 0 < x \le A_i)
,使得操作後

。給定

,問經過若干次操作後,能使得
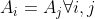
的話,它們的數值最多為多少。
直接的想法就是二分答案。設
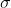
為經過若干次操作後最終每個數的一致值,定義
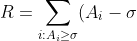, S = \sum_{i : A_i < \sigma}(\sigma-A_i)\frac{100}{100-k})
不難看出
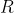
是
總供給量,

是
總需求量。若

則表示經過若干次操作後所有數皆等於
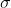
。若

則表示供過於求,即
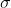
太低;若

則表示供不應求,即
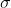
太高。應用二分法求最大的
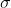
使得供求相符即可。
C: 給了一個有向無環圖,最多6個頂點,而且是完全圖。每條邊有要求流量最少最多值,和啟動值。設在邊
)
流量是

,啟動值
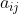
,則費用是

。求一個可行的網絡流,源是點1,匯是點

,需要符合上下限,要求流量最小,其次則要求費用最大。上下限最多是5,啟動費用最多是6。若沒有流量則毋需計算啟動費用。
明顯地數據範圍極小,可以考慮暴試。設
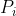
為第

點的注入量。對源點則有

。DFS狀態為
)
,當中

。此程序會嘗試從點
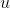
抽取
)
之間的注入量,加到

之中,然後按情況嘗試
, f(v+1, 1))
。當達到
)
即可中止。但嘗試量最多是
}{2}})
,肯定會超時。要應用一些prunning技巧。首先,當在狀態
)
的時候,若

已經大於最小流量值則中止嘗試。另,嘗試
)
的時候,應直接取走其注入量,並留意是否

,若否則中止搜索。
D: 待補。
沒有留言:
張貼留言