Easy: 給了一個正整數$N$和最初放在第$M$格的物件,你可作如下操作﹕
(1) 把$N$除以其任意一個質因數$p$,並捨棄其他不包含該物件的區間。
(2) 把格子向左或右旋轉一下。
目標是要把物件放在第一格。問最少需要多少步才可。
首先一定要把$N$進行質因數分解。另外需要留意的是,兩個操順序後並無一定關係。可以考慮先處理(2)再處理(1)之前,把$N/p$個等分疊在一起,其結果就等價於先進行(1)再進行(2)。所以可以知道答案必定是先進行若干次(也可能完全沒有)劃分,然後考慮向左或向右旋轉至第一格最划算的費用之和。另,因為$M$是以$1$開始算的,所以要處理劃分後的位置必須先把$M$變成以$0$開始才可。假設劃分後$N'=N/p$,$M'=M \bmod{N'}$。剩下來就是怎樣選取劃分了。因為$N \le 1000000$,其互不相同的質因數最多只有$8$個,因此可以考慮枚舉$8!$的劃分順序。
Medium: 給了$N$個正整數$R_1\cdots R_n$,求有多少數數列$A_1\cdots A_n$使得
(1) $\sum_{i=1}^n A_i = A_1 | A_2 \cdots | A_n$。
(2) $A_i \le R_i$。
答案取模$10^9+9$。$1 \le R_i \le 10^{18}$,$1 \le N \le 10 $。
很難的題目。但$N$不大應該可以有一些牽涉$2^N$的動態規劃。未決定狀態之前,首先第條件(1)要求$A_i$必須不能在某一個二進位有多於一個$1$,而且二進位之間的關係是離散的,因此可以考慮二進位$p$為狀態之一。條件(2)限制了決定那個$A_i$的第$p$位應該取值$1$。因為如果某個$A_i$設為$1$的話可能使得$A_i > R_i$;但只要某些條件下不論$A_i$的第$p$位取值多少都不影響條件(2)。例如$R_i = 10101001_{(2)}, A_i = 101*...._{(2)}$,$*$只可以放$0$,否則會違反了條件(2)。但若$R_i = 10101001_{(2)}, A_i = 100*...._{(2)}$,$*$可以取任意值而不影響條件(2)。廣義一點來說,舉凡$A_i$在$p$位以左是$R_i$的前綴的話,則$A_i$在第$p$位的取值必須受$R_i$的$p$位影響,否則可取任意值。這首先說明了兩件事。第一是$p$必須從左至右有依賴性,第二是可以引入一種狀態,標示有多少個$A_i$是不再符合前綴條件。因為$N \le 10$,這個狀態可以用$2^N$來表示。因此便有$f(p, b)$,算出有多少個可行的方案,使得$p$位以左的二進位都符合條件,並且$b$表示了所有不符合$R_i$的集合。注意為方便,我把位元的算法是以$1$為開始的。已知對所有$b$,$f(0, b) = 1$,因為$p = 0$表示決定$A_i$取值的程序已經完成了。否則,其狀態轉移方程如下﹕
\[
f(p, b) = f(p-1, b') + \sum_{i=1}^N v_i \times f(p-1, b_i'')
\]
其中$b'$是代表在$p$位取$0$的情況下,有多少原本還是前綴的$A_i$現在已經不是了,並加入到$b$之中。
$b''_i$則是決定把$A_i$的$p$位取值為$1$,並根據計算$b'$的方法重新計算$b''_i$有些不再是前綴(留意有些必須前綴的數因為第$p$位的$1$被$A_i$佔用了,所以必須在其第$p$位放置$0$並不再是前綴)。有時候$A_i$是前綴並且$R_i$的$p$位是$0$,因此它不能取值$1$,所以不能把$f(p-1, b_i'')$算進去的,因此$v_i = 0$,其餘情況下都是$v_i = 1$。因此本題可以在$O(2^N\times N^2M)$時間內解決,其中$M$表示最長有多少位元。因為$R_i \le 10^{18}$,因此$M \le 60$。
2011年7月24日 星期日
2011年7月22日 星期五
SRM 509 Div1 Easy + Medium
Easy: 給了一個不帶零的正整數$N$,可任意刪除數位(不能全部刪除、也可以不刪)但保持其原來次序,可得一集合$\mathcal{S}$。求$\sum_{i \in \mathcal{S}} i \bmod{9}$。例如$N = 123$則答案是
\[ 123 + 12 + 13 + 23 + 1 + 2 + 3 \equiv 177 \equiv 6 \pmod{9}\]
首先求取模$9$的意義。從上式可知
\[ 123 \equiv 1 + 2 + 3\pmod{9}\]
因此其實是問所有數位出現多少次,求和並取模。不難從例子發現,若$N$是一$L$位整數,則每個數位會出現$2^{L-1}$次。設$d(N)$是$N$的數位之和,則答案顯然是\[d(N)\times 2^{L-1} \bmod{9}\]
注意$2^{L-1}$可以超越整數範圍。
Medium: 給了一個字串$S$,並只給了幾種特定的操作,其操作形式只有三種。
(1) 在字串內刪除其中一個為$a$的字元,費用為$w_1$。
(2) 在字串內把其中一個為$a$的字元變成$b$,費用為$w_2$。
(3) 在字串加上一個為$a$的字元(可以在字串前後加上),費用為$w_3$。
現給予$R$種互不相同的操作,問把$S$變成迴文的最少費用。
處理這類字串成問題通常是考慮動態規劃狀態$F(x, y)$,即最少把子字串$S_{x\cdots y-1}$修改成迴文的最小費用。
先考慮簡化版問題﹕允許任意操作,並且一律費用為$1$。那麼其狀態轉移方程可以簡單描述成
\[F(x, y) = \begin{cases} 0 & \text{if $y-x \le 1$} \\ F(x+1, y-1) & \text{if $S_x = S_{y-1}$} \\ \min(F(x+1, y), F(x, y-1)) + 1 & \text{otherwise}\end{cases}\]
但套在這道問題又是否可行呢?首先留意到並非任意操作都可行,所以狀態方程必須因應對應字元而再設計。其次是任意操作的費用不再單純是$1$,意味著若把上述方程的費用$1$寫成通用的$W_{S_x,S_y}$,那麼其意義不只限於單次操作使得$S_x$和$S_y$匹配,而是可以經過一系列操作令$W_{S_x,S_y}$最少化。先考慮$C_{a,b}$,即最少費用把字元$a$修改成字元$b$,然後$W_{a,b}$則可經如下公式求得
\[W_{a,b} = \min_{c}\{C_{a,c} + C_{b,c}\}\]
這引伸了另一個問題﹕如何求$C_{a,b}$?可以想像到的是最短路算法。但首先留意求算需要周全考慮所有操作﹕如果只考慮改變字元的話是不夠的,因為可能最小費用操作可以循這種方式獲得﹕修改$\rightarrow$刪除$\rightarrow$加入$\rightarrow$修改。可見刪除和加入這兩種一般難以用最短路方式描述的操作是可以出現在最小費用操作的任意位置中。解決這個問題的一種思路是﹕何不可以把這兩種操作歸約成修改操作?留意兩種操作可以這樣看的﹕
(1)刪除﹕把字元$a$修改成字元$\emptyset$。
(1)加入﹕把字元$\emptyset$修改成字元$a$。
因此我們只需把空字元$\emptyset$列為可考慮修改字元的話,那麼$C_{a,b}$即可以用最短路
\[C_{a,b} = \min_{c \in \{\text{`a', `b', $\cdots$ `z', $\emptyset$}\}}\{C_{a,c} + C_{c, b}\}\]
求得,因此亦得到$W_{a,b}$。現在重新考慮狀態轉移方程,留意因為費用不再全部都是$1$的關係,因此我們把簡化版的方程的$S_x = S_y$情況一併歸約至一般情況之中,即可得解決本題的方程,如下﹕
\[F(x, y) = \begin{cases} 0 & \text{if $y-x \le 1$} \\ \min(F(x+1, y), F(x, y-1)) + W_{S_x,S_y} & \text{otherwise}\end{cases}\]
\[ 123 + 12 + 13 + 23 + 1 + 2 + 3 \equiv 177 \equiv 6 \pmod{9}\]
首先求取模$9$的意義。從上式可知
\[ 123 \equiv 1 + 2 + 3\pmod{9}\]
因此其實是問所有數位出現多少次,求和並取模。不難從例子發現,若$N$是一$L$位整數,則每個數位會出現$2^{L-1}$次。設$d(N)$是$N$的數位之和,則答案顯然是\[d(N)\times 2^{L-1} \bmod{9}\]
注意$2^{L-1}$可以超越整數範圍。
Medium: 給了一個字串$S$,並只給了幾種特定的操作,其操作形式只有三種。
(1) 在字串內刪除其中一個為$a$的字元,費用為$w_1$。
(2) 在字串內把其中一個為$a$的字元變成$b$,費用為$w_2$。
(3) 在字串加上一個為$a$的字元(可以在字串前後加上),費用為$w_3$。
現給予$R$種互不相同的操作,問把$S$變成迴文的最少費用。
處理這類字串成問題通常是考慮動態規劃狀態$F(x, y)$,即最少把子字串$S_{x\cdots y-1}$修改成迴文的最小費用。
先考慮簡化版問題﹕允許任意操作,並且一律費用為$1$。那麼其狀態轉移方程可以簡單描述成
\[F(x, y) = \begin{cases} 0 & \text{if $y-x \le 1$} \\ F(x+1, y-1) & \text{if $S_x = S_{y-1}$} \\ \min(F(x+1, y), F(x, y-1)) + 1 & \text{otherwise}\end{cases}\]
但套在這道問題又是否可行呢?首先留意到並非任意操作都可行,所以狀態方程必須因應對應字元而再設計。其次是任意操作的費用不再單純是$1$,意味著若把上述方程的費用$1$寫成通用的$W_{S_x,S_y}$,那麼其意義不只限於單次操作使得$S_x$和$S_y$匹配,而是可以經過一系列操作令$W_{S_x,S_y}$最少化。先考慮$C_{a,b}$,即最少費用把字元$a$修改成字元$b$,然後$W_{a,b}$則可經如下公式求得
\[W_{a,b} = \min_{c}\{C_{a,c} + C_{b,c}\}\]
這引伸了另一個問題﹕如何求$C_{a,b}$?可以想像到的是最短路算法。但首先留意求算需要周全考慮所有操作﹕如果只考慮改變字元的話是不夠的,因為可能最小費用操作可以循這種方式獲得﹕修改$\rightarrow$刪除$\rightarrow$加入$\rightarrow$修改。可見刪除和加入這兩種一般難以用最短路方式描述的操作是可以出現在最小費用操作的任意位置中。解決這個問題的一種思路是﹕何不可以把這兩種操作歸約成修改操作?留意兩種操作可以這樣看的﹕
(1)刪除﹕把字元$a$修改成字元$\emptyset$。
(1)加入﹕把字元$\emptyset$修改成字元$a$。
因此我們只需把空字元$\emptyset$列為可考慮修改字元的話,那麼$C_{a,b}$即可以用最短路
\[C_{a,b} = \min_{c \in \{\text{`a', `b', $\cdots$ `z', $\emptyset$}\}}\{C_{a,c} + C_{c, b}\}\]
求得,因此亦得到$W_{a,b}$。現在重新考慮狀態轉移方程,留意因為費用不再全部都是$1$的關係,因此我們把簡化版的方程的$S_x = S_y$情況一併歸約至一般情況之中,即可得解決本題的方程,如下﹕
\[F(x, y) = \begin{cases} 0 & \text{if $y-x \le 1$} \\ \min(F(x+1, y), F(x, y-1)) + W_{S_x,S_y} & \text{otherwise}\end{cases}\]
2011年7月15日 星期五
SRM 512 Div1 Easy + Medium
因為這次SRM是$2$的冪,所以題目分數也別出心裁的改為$2$的冪。
Easy: 假設某餐店只開$N$日,每日也賣出$M$款菜式。每日每款菜式的價格都有所不同。這餐廳有點古怪,要求你必須一天只買一款菜式;第$i$天買了第$j$款菜式的話必須在$i+7$天買第$j$款菜式;一旦你在第$i$天沒有光顧的話以後都不可以光顧該餐廳。你有$K$元在手,問最多能光顧這餐廳多少天。
算是比較容易的題。首先問題可以轉化為:能不能連續光顧$k$天?設這函數是$f(k)$的話我們就是求最大的$k$使得$f(k) = true$。當然由於$k$很小,線性枚舉所有$f(k)$即可。那麼判斷答案實在是很容易的–設$v_{i, j}^k$是在這連續$k$天內每星期$i$都買菜式$j$的總支出。判斷$f(k)$則只需檢查\[\sum_{i=1}^7 \min_{1\le j\le M}v_{i,j}^k \le K\]即可。
Medium: 一個泛費波那契數列是指任意正整數$f_0, f_1$為數列的首兩個元素,並且其數列遵從遞迴式$f_k = f_{k-1} + f_{k-2}, k > 1$。任何其子序列則稱為泛費波那契子數列。假設有一個正整數集$S$,當中有$N$個各不相同的整數。題目要求從$S$中取出兩個不相交的子集$A$和$B$,使得$A$和$B$皆為泛費波那契子數列,並且$A$的最大值必須少於$B$的最小值,而且$A$和$B$皆為上升序列。
乍看起來有點難。首先可以想到的是﹕能不能把$S$排序,然後劃分兩個子集$S_{1\cdots p}$、$S_{p+1\cdots N}$並分別在其中找出$A$和$B$?基於$N$不太大的關係,似乎有點可行,而且問題會簡化為從一個集合中找出最長的泛費波那契子數列。這個如何找呢?現在假設在$S$中找出$A$,可以試著想想枚舉。現在從$S$選出$S_i$和$S_j$,$i < j$,找出所在$S$中最長的泛費波那契子數列且必需包含$S_i$和$S_j$。不過包含$S_i$和$S_j$的子數列並非唯一,例如$\{1, 1, \mathbf 3, 5, \mathbf 8, 13\}$和$\{1, \mathbf 3, \mathbf 8, 11, 19\}$。但是可以留意兩件事﹕(1) $S_i$是數列的第幾個數並沒關係,只需要假定它是第一個就行;(2) 如果假定$S_j$是第$k$個數,則這個數列的存在性是唯一的,而且其唯一性是基於$S_i$之後的那個數。那麼我每只需枚舉$S_i$、$S_j$和$k$基本上憑求得序列的第二個數便可以確定序列。記得費波那契數的矩陣公式嗎?其實我們可以用同樣公式求得答案﹕
\[ \begin{bmatrix}F_k \\ F_{k-1} \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0\end{bmatrix}^{k-1} \begin{bmatrix}F_1 \\ F_0\end{bmatrix}\]
其中$F_k = S_j$,$F_0=S_i$而且$F_1$就是要求的答案。假設該式寫成
\[ \begin{bmatrix}S_j \\ F_{k-1} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d\end{bmatrix} \begin{bmatrix}F_1 \\ S_i\end{bmatrix}\]
則可以得到
\[ S_j = aF_1 + bS_i \]
然後可得$F_1 = \frac{S_j - bS_i}{a}$。於是若$F_1$有整數解,並且$F_1 > 0$,則可以憑$S_i, F_1, S_j$求得整條數列,然後利用set找出$S$內包含的所有序列元素,並從出找出最長的子序列。需留意的是不要重覆計算元素,例如$S_i = 1, S_j = 8, k = 4$(假設$k$是以$0$開始),$F_1=1$。另外枚舉子序列時若$F_1 < S_i$,就算$F_1\in S$也不應算為答案之一,因為題目要求答案序列是上升的。
在預計算$\begin{bmatrix} 1 & 1 \\ 1 & 0\end{bmatrix}^k$的情況下,這算法是$\tilde{O}(N^5)$的,但是也能足夠通過System test。至於$k$應該是多少?因為$S_i \le 10^8$,所以$k \le 50$足夠了。
Easy: 假設某餐店只開$N$日,每日也賣出$M$款菜式。每日每款菜式的價格都有所不同。這餐廳有點古怪,要求你必須一天只買一款菜式;第$i$天買了第$j$款菜式的話必須在$i+7$天買第$j$款菜式;一旦你在第$i$天沒有光顧的話以後都不可以光顧該餐廳。你有$K$元在手,問最多能光顧這餐廳多少天。
算是比較容易的題。首先問題可以轉化為:能不能連續光顧$k$天?設這函數是$f(k)$的話我們就是求最大的$k$使得$f(k) = true$。當然由於$k$很小,線性枚舉所有$f(k)$即可。那麼判斷答案實在是很容易的–設$v_{i, j}^k$是在這連續$k$天內每星期$i$都買菜式$j$的總支出。判斷$f(k)$則只需檢查\[\sum_{i=1}^7 \min_{1\le j\le M}v_{i,j}^k \le K\]即可。
Medium: 一個泛費波那契數列是指任意正整數$f_0, f_1$為數列的首兩個元素,並且其數列遵從遞迴式$f_k = f_{k-1} + f_{k-2}, k > 1$。任何其子序列則稱為泛費波那契子數列。假設有一個正整數集$S$,當中有$N$個各不相同的整數。題目要求從$S$中取出兩個不相交的子集$A$和$B$,使得$A$和$B$皆為泛費波那契子數列,並且$A$的最大值必須少於$B$的最小值,而且$A$和$B$皆為上升序列。
乍看起來有點難。首先可以想到的是﹕能不能把$S$排序,然後劃分兩個子集$S_{1\cdots p}$、$S_{p+1\cdots N}$並分別在其中找出$A$和$B$?基於$N$不太大的關係,似乎有點可行,而且問題會簡化為從一個集合中找出最長的泛費波那契子數列。這個如何找呢?現在假設在$S$中找出$A$,可以試著想想枚舉。現在從$S$選出$S_i$和$S_j$,$i < j$,找出所在$S$中最長的泛費波那契子數列且必需包含$S_i$和$S_j$。不過包含$S_i$和$S_j$的子數列並非唯一,例如$\{1, 1, \mathbf 3, 5, \mathbf 8, 13\}$和$\{1, \mathbf 3, \mathbf 8, 11, 19\}$。但是可以留意兩件事﹕(1) $S_i$是數列的第幾個數並沒關係,只需要假定它是第一個就行;(2) 如果假定$S_j$是第$k$個數,則這個數列的存在性是唯一的,而且其唯一性是基於$S_i$之後的那個數。那麼我每只需枚舉$S_i$、$S_j$和$k$基本上憑求得序列的第二個數便可以確定序列。記得費波那契數的矩陣公式嗎?其實我們可以用同樣公式求得答案﹕
\[ \begin{bmatrix}F_k \\ F_{k-1} \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0\end{bmatrix}^{k-1} \begin{bmatrix}F_1 \\ F_0\end{bmatrix}\]
其中$F_k = S_j$,$F_0=S_i$而且$F_1$就是要求的答案。假設該式寫成
\[ \begin{bmatrix}S_j \\ F_{k-1} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d\end{bmatrix} \begin{bmatrix}F_1 \\ S_i\end{bmatrix}\]
則可以得到
\[ S_j = aF_1 + bS_i \]
然後可得$F_1 = \frac{S_j - bS_i}{a}$。於是若$F_1$有整數解,並且$F_1 > 0$,則可以憑$S_i, F_1, S_j$求得整條數列,然後利用set找出$S$內包含的所有序列元素,並從出找出最長的子序列。需留意的是不要重覆計算元素,例如$S_i = 1, S_j = 8, k = 4$(假設$k$是以$0$開始),$F_1=1$。另外枚舉子序列時若$F_1 < S_i$,就算$F_1\in S$也不應算為答案之一,因為題目要求答案序列是上升的。
在預計算$\begin{bmatrix} 1 & 1 \\ 1 & 0\end{bmatrix}^k$的情況下,這算法是$\tilde{O}(N^5)$的,但是也能足夠通過System test。至於$k$應該是多少?因為$S_i \le 10^8$,所以$k \le 50$足夠了。
2011年6月19日 星期日
TCO 2011 Round 1
一年一度的比賽,就算再忙也要抽點時間出來比賽…
Easy:
給定了一個只帶o或x的隊列$A$,和兩個最被是空的隊列$B$和$C$,你可以進行如下四種操作﹕
1) B.enqueue(A.dequeue);
2) C.enqueue(A.dequeue);
3) A.enqueue(B.dequeue);
4) A.enqueue(C.dequeue);
問最少進行多少操作可以把$A$的內容變成指定的狀態?
不難發現一件事﹕在答案裡,$A$的最長後綴是最終狀態的前綴。剩下來的符號要怎樣處理?留意到為甚麼有兩條隊列嗎?這是因為你可以把非後綴的字元按o或x分別放到$B$和$C$,當剩下最長後綴時則按餘下的字元從$B$或$C$取出字元。那麼一個字元對應一出一入就是兩次操作,已是最少的了。
Medium:
給了一個$N$格的地圖,每格給出$p_i$,是為第$i$格變成泥濘的路的概率。保証第一格及第$N$格不會變成泥路。現在你可以向前一步或跳過一步。給定任何一整段路的狀態,你總是選定一個走法,使得跳進泥路的數量為最少。假設你現在站在第一格,到達第$N$格的時候,平均要走進多少個泥路?
其實又不是很難動態規劃,不過我卻想了很多不確定的東西。
關鍵的觀察是﹕如果你站在一個沒有泥的路,而前方有剛好$k$個泥路,那麼你最少可以踏過$\lfloor\frac{k}{2}\rfloor$個泥路。根據這個觀察可以這樣定義狀態函數$f(i, j, k)$,其中$i$是代表位置,$j$代表當前是第幾個連續的泥路,$k$是代表總共最少走過多少個泥路。那麼$f$即為該狀態的概率。其轉移方程則是﹕
\[ f(i+1, j+1, k+\delta) := f(i+1, j+1, k+\delta) + f(i, j, k) \times p_{i+1},\text{ where }\delta = \begin{cases}1 & \text{ if $j+1 \equiv 0 \pmod{2}$ } \\ 0 & \text{ otherwise}\end{cases}\]
\[ f(i+1, 0, k) := f(i+1, 0, k) + f(i, j, k) \times (1-p_{i+1})\]
而且$f(0, 0, 0) = 1$。那麼$O(N^3)$時間可以求出所有狀態,答案則是$\displaystyle\sum_{k=0}^N f(N-1, 0, k) \cdot k$。
注意本題有很簡單的$O(N)$的動態規劃。
Easy:
給定了一個只帶o或x的隊列$A$,和兩個最被是空的隊列$B$和$C$,你可以進行如下四種操作﹕
1) B.enqueue(A.dequeue);
2) C.enqueue(A.dequeue);
3) A.enqueue(B.dequeue);
4) A.enqueue(C.dequeue);
問最少進行多少操作可以把$A$的內容變成指定的狀態?
不難發現一件事﹕在答案裡,$A$的最長後綴是最終狀態的前綴。剩下來的符號要怎樣處理?留意到為甚麼有兩條隊列嗎?這是因為你可以把非後綴的字元按o或x分別放到$B$和$C$,當剩下最長後綴時則按餘下的字元從$B$或$C$取出字元。那麼一個字元對應一出一入就是兩次操作,已是最少的了。
Medium:
給了一個$N$格的地圖,每格給出$p_i$,是為第$i$格變成泥濘的路的概率。保証第一格及第$N$格不會變成泥路。現在你可以向前一步或跳過一步。給定任何一整段路的狀態,你總是選定一個走法,使得跳進泥路的數量為最少。假設你現在站在第一格,到達第$N$格的時候,平均要走進多少個泥路?
其實又不是很難動態規劃,不過我卻想了很多不確定的東西。
關鍵的觀察是﹕如果你站在一個沒有泥的路,而前方有剛好$k$個泥路,那麼你最少可以踏過$\lfloor\frac{k}{2}\rfloor$個泥路。根據這個觀察可以這樣定義狀態函數$f(i, j, k)$,其中$i$是代表位置,$j$代表當前是第幾個連續的泥路,$k$是代表總共最少走過多少個泥路。那麼$f$即為該狀態的概率。其轉移方程則是﹕
\[ f(i+1, j+1, k+\delta) := f(i+1, j+1, k+\delta) + f(i, j, k) \times p_{i+1},\text{ where }\delta = \begin{cases}1 & \text{ if $j+1 \equiv 0 \pmod{2}$ } \\ 0 & \text{ otherwise}\end{cases}\]
\[ f(i+1, 0, k) := f(i+1, 0, k) + f(i, j, k) \times (1-p_{i+1})\]
而且$f(0, 0, 0) = 1$。那麼$O(N^3)$時間可以求出所有狀態,答案則是$\displaystyle\sum_{k=0}^N f(N-1, 0, k) \cdot k$。
注意本題有很簡單的$O(N)$的動態規劃。
2011年4月28日 星期四
Codeforces #78
題目出乎意料之外的難…
A: 給定三行字串 $s_1, s_2, s_3$ 問其帶母音數是否等於 $(5, 7, 5)$ 。送分題。
B: 現在有 $7 \le N \le 100$ 個人圍成一圈,現在要分派7種顏色的復活蛋,要求是每種顏色的復活蛋必須至少有一人被分發,而且任意連續四人分配到的必須是四種不同顏色的蛋。給出一種可能分發復活蛋的方案。
先把顏色變成數字 $[1, 7]$ 。因為題目保証答案永遠存在,不妨先考慮 $N = 8$ 的情況。如果第1至7人分別得到顏色為 $1, 2, \cdots 7$ 的復活蛋的話,哪麼第8人應該拿甚麼顏色?注意第一個條件已經滿足了,要讓第二條件滿足,關鍵在如何分配給第8個人。若過他往前看3人拿的顏色,應是 $\{1, 2, 3\}$ ;往後看的話則是 $\{5, 6, 7\}$ ,故他只能取得顏色為 $[1, 7] - \{1, 2, 3, 5, 6, 7\} = \{4\}$ 的蛋。若是第9人呢?首先按同樣道理往前看已決定他不能取顏色為 $\{1, 2, 3\}$ 的復活蛋,但往後看的話現在則不能拿到 $\{4, 6, 7\}$ 的蛋,故只剩下顏色為5的蛋可取。注意往前再分析第8人時它本來向前看的顏色是 $\{1, 2, 3\}$ 現在變成了 $\{5, 1, 2\}$ 但條件仍舊滿足。細心再推論之下其實派蛋的方法是遵從這種數列﹕ $(1, 2, 3, 4, 5, 6, 7, 4, 5, 6, 7, 4, 5, 6, 7, 4, 5, 6, 7\cdots)$ 。
C: 問有 $N$ 條木棒,各長度皆為 $M$ 。現在兩人輪流玩遊戲。每一回合其中一人必須選擇一根木棒,折成多於一條均等整數長度的木棒,且其長度不得少於 $K$ 。沒法進行此一操作者為負方。現給定 $N, M, K$ 決定誰是勝方。
二人博弈問題。先不想 $M, K$ 的,考慮 $N$ 對賽局的影響。把木棒分成一雙雙,可以發現如果 $N$ 是偶數的話當先手選擇某一雙的一根木棒毅行操作,對方可選該雙的另一根木棒進行同樣的操作,因此先手必負。如果 $N$ 是奇數的話,根據同樣道理可知先手最後被迫對剩下的一根長度為 $M$ 的木棒進行操作。
因此遊戲在 $N$ 是奇數的情況下可以視作只有一根木棒的遊戲。同樣對 $N$ 為偶數的特性,先手必須盡量把木棒分成雙數等分的木棒,且長度至少為 $K$ ,此舉可以讓對方陷入必敗局。若不存在這樣的一步,則直接看看能否把木棒分拆即可。因為通過分拆成剛好大於 $K$ 的木棒後對方必不能再進行操作,因此能找到這樣的分拆必也可以直接勝出。需要注意 $N = K = 1$ 的情況: $M = 1$ 時必敗, $M > 1$ 時必勝。
D: 簡單點說就是問一個以邊長為1的正六邊形舖密的蜂巢狀世界,假設你站在其中一個正六邊形的中點為座標的原點,視野是一半徑為 $R$ 的圓,問有多少個半正六邊形是被這圓所包含的?包含的定義是指該正六邊形內任意一點必須與原點距離少於等於 $R$ 。下圖展示了 $R = 6$ 所包含的31個正六邊形﹕

紅線是視野,橙色的正六邊形是被包含的正六邊形。
做法是考慮圓形上的一個象限,如下圖﹕

然後沿著從象限左至右 $O(1)$ 求新一個直行能最盡延伸的正六邊形,如下圖﹕

利用上下對稱原理可計算該直行有多少個被包含的正六邊形,因此半個圓的答案 $S$ 可以快速求得。然後再用左右對稱的原計算答案 $C = 2S - S_1$ 當中 $S_1$ 是中心那個直行包含了多少個正六邊形,因為 $2S$ 重覆計算了該行的數量。
注意﹕枚舉移動格子的時候不應用加法更新縱座標,因為對於 $N$ 較大的時候,加法更新會引致精度問題﹕如果能重新計算距離的話則可以防止精度問題發生。
[更新]所謂的重新計算是基於對格子進行標號,如下圖﹕

那麼對於偶數直行的縱座標即是 $L_y \times \sqrt{3}$ ,奇數行的則是 $L_y \times \sqrt{3} + \frac{\sqrt{3}}{2}$ 。
E: 給了一個 $N\times N$ 的地圖。每個格子要麼是一個房間,要麼是一個毒氣罐且佔滿整個格子。現在某些毒氣罐洩漏了毒氣,每一時間單位向鄰接格子擴散。最初每個房間含最多9人,每個房間含逃生倉最多9個。人們以每一個時間單位向鄰接房間移動,如在該房間內遇上未佔用的逃生倉即可進內並不受毒氣毒害。退化情況下,如毒氣和人員能在同一時間內到達未佔用逃生倉的房間,則該人亦能佔用逃生倉而不受毒氣侵害。更糟糕的時,整個地方會在剛好 $t$ 個時間單位後發生大爆炸,幸運的是逃生倉內的人亦不受損害。求最多有多少人在 $t$ 秒後仍然生存。
先不考慮毒氣的擴散,問題就是某些地方有人,某些地方有逃生倉,求 $t$ 步內可以滿足最多生存人數。不難留意 $N \times N$ 的地圖等價於格網圖,先設為 $G$ ,如下圖所示﹕

現在問題即是求限制 $t$ 步的最大流,其中 $t$ 步限制即可以利用層圖解決。做法是把 $G$ 複製成 $t+1$ 份 $G_0, G_1, \cdots G_t$,如下圖﹕

然後把 $G_t$ 的所有邊移去,對於 $0 \le i < t$ , $G_i$ 的邊 $(u_i, v_i)$ 變成 $(u_i, v_{i+1})$ 。那麼上述例子的圖大概會變成下圖﹕

然後把源點 $s$ 連上 $G_0$ 上的所有點,並設容量為最初地圖上的人員數。對於帶逃生倉的點 $v \in G$ ,把 $v_i$ 連上局部匯 $t_v$ 並設容量為逃生倉的數量。最後把所有 $t_v$ 連上匯 $t$ ,同樣設容量為逃生倉的數量。最大流即可求得答案。
如果加上毒氣的話怎麼辦?首先是依毒氣的流動計算 $G$ 任何一個點 $v$ 至少甚麼時候會被毒氣侵襲(設為 $\infty$ 或 $t+1$ 即代表不受影響),設該數值為 $L_v$ 。然後對於所有 $G_i, i \le L_v$ 把點 $v_i$ 的所有邊都移除即可。
至於本題的最大流應該用甚麼算法去解決,先考慮點的數量。用層圖的方法最多有 $(t+2)N^2 + N + 2$ 。因為 $ t \le 60, N \le 10$ ,點的數量最多可達 $6212$ 個。但留意此層圖非常稀疏,因此粗略計算,邊的數量最多為 $6(t+1)N^2 + N$ ,仍是線性數量的。而且答案最大為 $9\times 10^2 = 900$ ,因此用Ford-Fulkerson算法,於 $O(Ef)$ 的複雜度下運行時間仍然讓人滿意。
A: 給定三行字串 $s_1, s_2, s_3$ 問其帶母音數是否等於 $(5, 7, 5)$ 。送分題。
B: 現在有 $7 \le N \le 100$ 個人圍成一圈,現在要分派7種顏色的復活蛋,要求是每種顏色的復活蛋必須至少有一人被分發,而且任意連續四人分配到的必須是四種不同顏色的蛋。給出一種可能分發復活蛋的方案。
先把顏色變成數字 $[1, 7]$ 。因為題目保証答案永遠存在,不妨先考慮 $N = 8$ 的情況。如果第1至7人分別得到顏色為 $1, 2, \cdots 7$ 的復活蛋的話,哪麼第8人應該拿甚麼顏色?注意第一個條件已經滿足了,要讓第二條件滿足,關鍵在如何分配給第8個人。若過他往前看3人拿的顏色,應是 $\{1, 2, 3\}$ ;往後看的話則是 $\{5, 6, 7\}$ ,故他只能取得顏色為 $[1, 7] - \{1, 2, 3, 5, 6, 7\} = \{4\}$ 的蛋。若是第9人呢?首先按同樣道理往前看已決定他不能取顏色為 $\{1, 2, 3\}$ 的復活蛋,但往後看的話現在則不能拿到 $\{4, 6, 7\}$ 的蛋,故只剩下顏色為5的蛋可取。注意往前再分析第8人時它本來向前看的顏色是 $\{1, 2, 3\}$ 現在變成了 $\{5, 1, 2\}$ 但條件仍舊滿足。細心再推論之下其實派蛋的方法是遵從這種數列﹕ $(1, 2, 3, 4, 5, 6, 7, 4, 5, 6, 7, 4, 5, 6, 7, 4, 5, 6, 7\cdots)$ 。
C: 問有 $N$ 條木棒,各長度皆為 $M$ 。現在兩人輪流玩遊戲。每一回合其中一人必須選擇一根木棒,折成多於一條均等整數長度的木棒,且其長度不得少於 $K$ 。沒法進行此一操作者為負方。現給定 $N, M, K$ 決定誰是勝方。
二人博弈問題。先不想 $M, K$ 的,考慮 $N$ 對賽局的影響。把木棒分成一雙雙,可以發現如果 $N$ 是偶數的話當先手選擇某一雙的一根木棒毅行操作,對方可選該雙的另一根木棒進行同樣的操作,因此先手必負。如果 $N$ 是奇數的話,根據同樣道理可知先手最後被迫對剩下的一根長度為 $M$ 的木棒進行操作。
因此遊戲在 $N$ 是奇數的情況下可以視作只有一根木棒的遊戲。同樣對 $N$ 為偶數的特性,先手必須盡量把木棒分成雙數等分的木棒,且長度至少為 $K$ ,此舉可以讓對方陷入必敗局。若不存在這樣的一步,則直接看看能否把木棒分拆即可。因為通過分拆成剛好大於 $K$ 的木棒後對方必不能再進行操作,因此能找到這樣的分拆必也可以直接勝出。需要注意 $N = K = 1$ 的情況: $M = 1$ 時必敗, $M > 1$ 時必勝。
D: 簡單點說就是問一個以邊長為1的正六邊形舖密的蜂巢狀世界,假設你站在其中一個正六邊形的中點為座標的原點,視野是一半徑為 $R$ 的圓,問有多少個半正六邊形是被這圓所包含的?包含的定義是指該正六邊形內任意一點必須與原點距離少於等於 $R$ 。下圖展示了 $R = 6$ 所包含的31個正六邊形﹕

紅線是視野,橙色的正六邊形是被包含的正六邊形。
做法是考慮圓形上的一個象限,如下圖﹕

然後沿著從象限左至右 $O(1)$ 求新一個直行能最盡延伸的正六邊形,如下圖﹕

利用上下對稱原理可計算該直行有多少個被包含的正六邊形,因此半個圓的答案 $S$ 可以快速求得。然後再用左右對稱的原計算答案 $C = 2S - S_1$ 當中 $S_1$ 是中心那個直行包含了多少個正六邊形,因為 $2S$ 重覆計算了該行的數量。
注意﹕枚舉移動格子的時候不應用加法更新縱座標,因為對於 $N$ 較大的時候,加法更新會引致精度問題﹕如果能重新計算距離的話則可以防止精度問題發生。
[更新]所謂的重新計算是基於對格子進行標號,如下圖﹕

那麼對於偶數直行的縱座標即是 $L_y \times \sqrt{3}$ ,奇數行的則是 $L_y \times \sqrt{3} + \frac{\sqrt{3}}{2}$ 。
E: 給了一個 $N\times N$ 的地圖。每個格子要麼是一個房間,要麼是一個毒氣罐且佔滿整個格子。現在某些毒氣罐洩漏了毒氣,每一時間單位向鄰接格子擴散。最初每個房間含最多9人,每個房間含逃生倉最多9個。人們以每一個時間單位向鄰接房間移動,如在該房間內遇上未佔用的逃生倉即可進內並不受毒氣毒害。退化情況下,如毒氣和人員能在同一時間內到達未佔用逃生倉的房間,則該人亦能佔用逃生倉而不受毒氣侵害。更糟糕的時,整個地方會在剛好 $t$ 個時間單位後發生大爆炸,幸運的是逃生倉內的人亦不受損害。求最多有多少人在 $t$ 秒後仍然生存。
先不考慮毒氣的擴散,問題就是某些地方有人,某些地方有逃生倉,求 $t$ 步內可以滿足最多生存人數。不難留意 $N \times N$ 的地圖等價於格網圖,先設為 $G$ ,如下圖所示﹕

現在問題即是求限制 $t$ 步的最大流,其中 $t$ 步限制即可以利用層圖解決。做法是把 $G$ 複製成 $t+1$ 份 $G_0, G_1, \cdots G_t$,如下圖﹕

然後把 $G_t$ 的所有邊移去,對於 $0 \le i < t$ , $G_i$ 的邊 $(u_i, v_i)$ 變成 $(u_i, v_{i+1})$ 。那麼上述例子的圖大概會變成下圖﹕

然後把源點 $s$ 連上 $G_0$ 上的所有點,並設容量為最初地圖上的人員數。對於帶逃生倉的點 $v \in G$ ,把 $v_i$ 連上局部匯 $t_v$ 並設容量為逃生倉的數量。最後把所有 $t_v$ 連上匯 $t$ ,同樣設容量為逃生倉的數量。最大流即可求得答案。
如果加上毒氣的話怎麼辦?首先是依毒氣的流動計算 $G$ 任何一個點 $v$ 至少甚麼時候會被毒氣侵襲(設為 $\infty$ 或 $t+1$ 即代表不受影響),設該數值為 $L_v$ 。然後對於所有 $G_i, i \le L_v$ 把點 $v_i$ 的所有邊都移除即可。
至於本題的最大流應該用甚麼算法去解決,先考慮點的數量。用層圖的方法最多有 $(t+2)N^2 + N + 2$ 。因為 $ t \le 60, N \le 10$ ,點的數量最多可達 $6212$ 個。但留意此層圖非常稀疏,因此粗略計算,邊的數量最多為 $6(t+1)N^2 + N$ ,仍是線性數量的。而且答案最大為 $9\times 10^2 = 900$ ,因此用Ford-Fulkerson算法,於 $O(Ef)$ 的複雜度下運行時間仍然讓人滿意。
2011年4月26日 星期二
Codeforces #26 D Tickets
題意﹕現在有一個計數器,數值最初為 $k$ ,並有兩個按鈕﹕一是可以讓計數器加一,一是可以讓計數器減一。現在你可以按 $n$ 次加一 $m$ 次減一,若你選取操作的排例的概率是均等,那麼有多少機會使得你在操作中途計數器總是非負?
首先,用圖表的方式去想。假定橫軸是操作的時序,縱軸代表計數器在某個時刻的數值,那麼一個操作順序剛好表示了一副折線圖。像如下的圖代表操作不會引致負數﹕

順道留意﹕終點永遠在座標 $(n+m, n+k-m)$ 。如失敗的話,折線圖必然會與橫線 $y = -1$ 相交,如下圖所示﹕

首先,所有折線圖的數量是 $T = \binom{n+m}{n}$ ,來源可以想像成﹕在 $n + m$ 個時序中任意取 $n$ 個時序進行加一,同樣道理可得出 $\binom{n+m}{m} = \binom{n+m}{n}$ 。如果我們能求所有與 $y = -1$ 相交的折線圖的數量 $S$ ,那麼答案就是 $1 - \frac{S}{T}$ 。說來倒是很容易,但是礙於限制,我們不能直接用公式求算 $S$ 的數量。1978年Cohen利用「反射原理」解決了類同問題,我們也可以試著利用此原理解決問題。
首先留意任何與 $y=-1$ 相交的折線圖,其最後與 $y = -1$ 相交的點,之後必然最終上升至 $(n+m, n+k-m)$ (留意它並非直線上升,中途可能還會下跌,但永遠不會跌至負數值)。這條線從相交點計起長度是 $n+k-m+1$ 。那麼我們試著把這條線「反射」一下,它則一下子掉到 $(n+m, -1-n-k+m-1) = (n+m, m-n-k-2)$ 。例子如下:

藍色點是反射起點,藍色虛線是反射線。留意線過部份反射後的折線圖與原來的圖是一一對應的。另外,新的折線圖擺脫了橫線相交的限制,因為通過反射後折線圖已經肯定是與橫線 $y=-1$ 相交,因此可以看作成在 $(n+m, m-k-n-2)$ 出發,逆時序的加一減一,直至到達 $(0, k)$ 有多少操作,其且每一個圖與原來和橫線相交的圖一一對應。問題是,經這種轉換後我們不清楚被允計使用多少次加一與減一所組成的。設我們被允許 $a$ 次加一 $b$ 次減一,利用反射原理的一一對應關係,我們得到如下式﹕
\[\left\{ \begin{array}{ll} a+b = n+m & \quad \text{(width restriction)}\\ k+a-b = m-n-k-2 & \quad \text{(height restriction)}\\ \end{array} \right.\]
因此我們可得 $a = m - k - 1$ 。而新圖的數量則是 $\binom{n+m}{a} = \binom{n+m}{m-k-1}$ 。又因為每一個新折線圖與原來和橫線相交的圖一一對應,故得 $S = \binom{n+m}{m-k-1}$ 。因此本題的答案是
\[1-\frac{S}{T}=1-\frac{\binom{n+m}{m-k-1}}{\binom{n+m}{n}} = 1-\frac{(m-k)(m-k+1)\cdots m}{(n+1)(n+2)\cdots (n+k+1)}\]
如欲清楚更多反射原理的資料,請參考[1]。
[1] D. I. A. Cohen, Basic Techniques of Combinatorial Theory, John Wiley and Sons, New York (1978).
首先,用圖表的方式去想。假定橫軸是操作的時序,縱軸代表計數器在某個時刻的數值,那麼一個操作順序剛好表示了一副折線圖。像如下的圖代表操作不會引致負數﹕

順道留意﹕終點永遠在座標 $(n+m, n+k-m)$ 。如失敗的話,折線圖必然會與橫線 $y = -1$ 相交,如下圖所示﹕

首先,所有折線圖的數量是 $T = \binom{n+m}{n}$ ,來源可以想像成﹕在 $n + m$ 個時序中任意取 $n$ 個時序進行加一,同樣道理可得出 $\binom{n+m}{m} = \binom{n+m}{n}$ 。如果我們能求所有與 $y = -1$ 相交的折線圖的數量 $S$ ,那麼答案就是 $1 - \frac{S}{T}$ 。說來倒是很容易,但是礙於限制,我們不能直接用公式求算 $S$ 的數量。1978年Cohen利用「反射原理」解決了類同問題,我們也可以試著利用此原理解決問題。
首先留意任何與 $y=-1$ 相交的折線圖,其最後與 $y = -1$ 相交的點,之後必然最終上升至 $(n+m, n+k-m)$ (留意它並非直線上升,中途可能還會下跌,但永遠不會跌至負數值)。這條線從相交點計起長度是 $n+k-m+1$ 。那麼我們試著把這條線「反射」一下,它則一下子掉到 $(n+m, -1-n-k+m-1) = (n+m, m-n-k-2)$ 。例子如下:

藍色點是反射起點,藍色虛線是反射線。留意線過部份反射後的折線圖與原來的圖是一一對應的。另外,新的折線圖擺脫了橫線相交的限制,因為通過反射後折線圖已經肯定是與橫線 $y=-1$ 相交,因此可以看作成在 $(n+m, m-k-n-2)$ 出發,逆時序的加一減一,直至到達 $(0, k)$ 有多少操作,其且每一個圖與原來和橫線相交的圖一一對應。問題是,經這種轉換後我們不清楚被允計使用多少次加一與減一所組成的。設我們被允許 $a$ 次加一 $b$ 次減一,利用反射原理的一一對應關係,我們得到如下式﹕
\[\left\{ \begin{array}{ll} a+b = n+m & \quad \text{(width restriction)}\\ k+a-b = m-n-k-2 & \quad \text{(height restriction)}\\ \end{array} \right.\]
因此我們可得 $a = m - k - 1$ 。而新圖的數量則是 $\binom{n+m}{a} = \binom{n+m}{m-k-1}$ 。又因為每一個新折線圖與原來和橫線相交的圖一一對應,故得 $S = \binom{n+m}{m-k-1}$ 。因此本題的答案是
\[1-\frac{S}{T}=1-\frac{\binom{n+m}{m-k-1}}{\binom{n+m}{n}} = 1-\frac{(m-k)(m-k+1)\cdots m}{(n+1)(n+2)\cdots (n+k+1)}\]
如欲清楚更多反射原理的資料,請參考[1]。
[1] D. I. A. Cohen, Basic Techniques of Combinatorial Theory, John Wiley and Sons, New York (1978).
Topcoder SRM 504 DIV 1 Easy + Medium
題目出得不錯,也挺容易,唯獨最後15分鐘伺服器又出問題,不算rating了。Topcoder應該考慮是否調低參賽者的註冊人數,免得同類事故再發生。
Easy: 大意是有一個 $01$ 字串 $S$ 重覆 $K$ 遍,即 $S' = \underbrace{S\cdots S}_{K\text{ times}}$ 。每一回合把 $S'$ 的首個字元拿出來,如果是 $0$ 的話,則把 $S'$ 餘下的元字順序倒換。如果是 $1$ 的話則把 $S'$ 的字元取逆,即 $S'_i := 1 - S'_i$ 。問通過這個過程裡你能抽到多少個 $1$ 的字元。保証 $S'$ 最多帶 $100000$ 個字元。
做法是保留兩個指針兩個變量。指針一指首一指尾,變量決定元素取前或後和數值需否取逆。然後…就是做。或者可以用STL的deque<T>。
Medium:對於一個 $N \times M$ 的 $01$ -板塊,它依如下程序段修改其內容。
現在有一輸出 $O$ ,問有多少個輸入可以經以上程序段後得出它。答案取模 $1000000007$ 。
留意幾件事即可。
1. 根據程序段,首行是固定的。
2. 第 $1 \le i < N$ 行的結果 $O_i$ 由 $O_{i-1}$ 來決定的,因為本來的輸入已經被程序段毀掉了。
3. 實際是求對於 $0 \le i \le N-2$ 由 $O_i$ 決定 $O_{i+1}$ 的輸入有多少種。
4. 根據程序段,操作是自左向右處理的。只要把 $O_{i+1}$ 自右至左進行逆操作,理應是要求輸入行有哪些字元可以是任意字元。假設該行有 $K$ 個任意字元,那麼結答案則可以再乘上 $2^K$ 。
5. 哪些逆操作可以決定某元素是否任意字元?留意只有 $(0, 1)$ 和 $(1, 0)$ 才會硬把兩個字元改成一種顏色,其逆操作不能判斷原來的字元。 $(1, 1)$ 的逆操作則與本來操作一樣。 $(0, 0)$ 逆操也作就是甚麼都不幹。
6. 甚麼時候是沒有解?就是進行 $(0, 1)$ 和 $(1, 0)$ 的逆操作時對兩個應修改元素的值與進行其操作後不相符。此時大可以回傳0。
Easy: 大意是有一個 $01$ 字串 $S$ 重覆 $K$ 遍,即 $S' = \underbrace{S\cdots S}_{K\text{ times}}$ 。每一回合把 $S'$ 的首個字元拿出來,如果是 $0$ 的話,則把 $S'$ 餘下的元字順序倒換。如果是 $1$ 的話則把 $S'$ 的字元取逆,即 $S'_i := 1 - S'_i$ 。問通過這個過程裡你能抽到多少個 $1$ 的字元。保証 $S'$ 最多帶 $100000$ 個字元。
做法是保留兩個指針兩個變量。指針一指首一指尾,變量決定元素取前或後和數值需否取逆。然後…就是做。或者可以用STL的deque<T>。
Medium:對於一個 $N \times M$ 的 $01$ -板塊,它依如下程序段修改其內容。
For i = 0 to N-2:
For j = 0 to M-2:
//Get the current colors of cells (i,j) and (i,j+1)
A = Grid(i,j) , B = Grid(i,j+1)
If (A,B) == (0, 0) Then:
Do nothing.
EndIf
If (A,B) == (1, 0) Then:
Mark cells (i+1,j) and (i+1,j+1) as 1.
EndIf
If (A,B) == (0, 1) Then:
Mark cells (i+1,j) and (i+1,j+1) as 0.
EndIf
if (A,B) == (1, 1) Then:
Swap the content in cells (i+1,j) and (i+1,j+1).
EndIf
EndFor
EndFor
現在有一輸出 $O$ ,問有多少個輸入可以經以上程序段後得出它。答案取模 $1000000007$ 。
留意幾件事即可。
1. 根據程序段,首行是固定的。
2. 第 $1 \le i < N$ 行的結果 $O_i$ 由 $O_{i-1}$ 來決定的,因為本來的輸入已經被程序段毀掉了。
3. 實際是求對於 $0 \le i \le N-2$ 由 $O_i$ 決定 $O_{i+1}$ 的輸入有多少種。
4. 根據程序段,操作是自左向右處理的。只要把 $O_{i+1}$ 自右至左進行逆操作,理應是要求輸入行有哪些字元可以是任意字元。假設該行有 $K$ 個任意字元,那麼結答案則可以再乘上 $2^K$ 。
5. 哪些逆操作可以決定某元素是否任意字元?留意只有 $(0, 1)$ 和 $(1, 0)$ 才會硬把兩個字元改成一種顏色,其逆操作不能判斷原來的字元。 $(1, 1)$ 的逆操作則與本來操作一樣。 $(0, 0)$ 逆操也作就是甚麼都不幹。
6. 甚麼時候是沒有解?就是進行 $(0, 1)$ 和 $(1, 0)$ 的逆操作時對兩個應修改元素的值與進行其操作後不相符。此時大可以回傳0。
2011年4月17日 星期日
Topcoder Member SRM 503 Easy
Codeforces #74
上次腦殘之後,人品突然挺好的…
A: 問每個參賽者的答題的分數,成功及失敗的挑戰,問比賽的贏家是誰。保証只有一個贏家。極點頹題。
B: 捉迷藏遊戲。查票員會從火車的頭卡至尾卡不斷的來回檢查,每個時刻只會移動一個車廂。逃票人則在火車移動的時候選擇留守同一車廂,或向附近一車廂移動。如果火車停站了,他可以先行離開車廂,並能進入任意一個車廂,假設這個步驟是不看耗時的。現在給了查票員和逃票人的最初位置,和查票員的行走方向,並保証最後一個時刻是終點站,問給定每個時刻火車是到站還是行走中,逃票人能否不被查票員逮著?即使一定被逮到,最遲必定在甚麼時候被逮著?其實處理上有點麻煩的,對於火車移動的時刻,逃票人的移動有最多3個選擇,並且對查票員的前後移動跟逃票人的距離進行排序,然後往最遠距離的一點移動。如果該距離只能是0的話則會被抓。對於火車停站的時刻,逃票人永遠可以躲在查票員背對的盡頭的車廂,當然,若查票員已站在頭卡或尾卡,則必須站在該對面盡頭即可。寫的時候人品超好,一次就寫對了…
C: 問一個 $N \times M$ 的板,問有多少條不同的桌球的彈道。球的移動遵從45度的斜線運動,碰壁的話會改變方向。卡了很久沒能找到 $O(1)$ 算式…至放棄時想想不如直接寫程序計算一些數值再想想,但之前已經想到一件事﹕彈道必先會經過第一行的其中一個格子。寫的時候想到不用逐步移動,直接可以算出碰在那了。然後在第一行的起點經過剛好3次就能保証遍歷一條完整的彈道。跑的時候跟手算答案一致,無聊試試最大的情況 $N = M = 10^6$ ,竟然不消半晌就跑出答案了﹗後來猛然醒起寫的時候那個直接算出碰撞點可以讓算法變得很高效的…直接提交並通過了。早知一早放棄手寫,然後寫程序找答案還來得有效。後來看tourist的答案… $\text{gcd}(N-1, M-1)+1$ …徹底輸了。
D, E: 待補
A: 問每個參賽者的答題的分數,成功及失敗的挑戰,問比賽的贏家是誰。保証只有一個贏家。極點頹題。
B: 捉迷藏遊戲。查票員會從火車的頭卡至尾卡不斷的來回檢查,每個時刻只會移動一個車廂。逃票人則在火車移動的時候選擇留守同一車廂,或向附近一車廂移動。如果火車停站了,他可以先行離開車廂,並能進入任意一個車廂,假設這個步驟是不看耗時的。現在給了查票員和逃票人的最初位置,和查票員的行走方向,並保証最後一個時刻是終點站,問給定每個時刻火車是到站還是行走中,逃票人能否不被查票員逮著?即使一定被逮到,最遲必定在甚麼時候被逮著?其實處理上有點麻煩的,對於火車移動的時刻,逃票人的移動有最多3個選擇,並且對查票員的前後移動跟逃票人的距離進行排序,然後往最遠距離的一點移動。如果該距離只能是0的話則會被抓。對於火車停站的時刻,逃票人永遠可以躲在查票員背對的盡頭的車廂,當然,若查票員已站在頭卡或尾卡,則必須站在該對面盡頭即可。寫的時候人品超好,一次就寫對了…
C: 問一個 $N \times M$ 的板,問有多少條不同的桌球的彈道。球的移動遵從45度的斜線運動,碰壁的話會改變方向。卡了很久沒能找到 $O(1)$ 算式…至放棄時想想不如直接寫程序計算一些數值再想想,但之前已經想到一件事﹕彈道必先會經過第一行的其中一個格子。寫的時候想到不用逐步移動,直接可以算出碰在那了。然後在第一行的起點經過剛好3次就能保証遍歷一條完整的彈道。跑的時候跟手算答案一致,無聊試試最大的情況 $N = M = 10^6$ ,竟然不消半晌就跑出答案了﹗後來猛然醒起寫的時候那個直接算出碰撞點可以讓算法變得很高效的…直接提交並通過了。早知一早放棄手寫,然後寫程序找答案還來得有效。後來看tourist的答案… $\text{gcd}(N-1, M-1)+1$ …徹底輸了。
D, E: 待補
Codeforces Round #67
本人極其腦殘的一次比賽,幸好不算rating,否則糟榚。
A: 問兩整數 $A,B$ 把零除去後,其和是否等於 $A+B$ 把零除去的值。頹。
B: 有一社交網站(名字…你懂的),有三項動作﹕(1)X在Y的留言板上留言 (+15分) (2)X在Y的貼文內留言 (+10分) (3)X讚Y的post。你知道你名字和一系列的動作,每項動作將會替X和Y添加括號內所述的分數。問對於你來說,跟你互動而分數最多至最少的的人的排序是怎樣。即使沒跟你互動都要顯示出來。我錯了幾次是因為沒看到分數是相對於自己…
C: $Q$ 次詢問,每次問區間 $[a, b]$ 內 $\text{gcd}(X, Y)$ 最大的因數。腦殘的爆發點,明明 $O(Q\sqrt{\text{gcd}(X, Y)})$ 可以搞定,我卻寫了質素因數分解,二分找答案…當然是趕急的寫,最後也過不了…
D: 有 $N$ 個小數組,現有 $M$ 個標號,把各標號對應的數組接了起來,問其最大連續子序列和最大是多少。又一腦殘點,漏了個很容易考慮到的情況。首先對每個小數組,求出其左連接最大和,數組和,及右連接最大和。那麼對每標號則考當前和加上數組和是否單調上升。若是則加上數組和並繼續,否則應先更近答案,皆因當前數值可至少加上該標號的左連接最大和使得更大但沒法再向右繼續;之後應從甚麼數開始再繼續?答案就是數組和或右連接最大和之間的最大值。但是注意,每次輸入一個新標號之後,其小數組的最大連續子序列和可能就是唯一答案,必須同時預先比對答案和其數值。我漏了處理這個,連pretest都過不了。
E: 待補。
A: 問兩整數 $A,B$ 把零除去後,其和是否等於 $A+B$ 把零除去的值。頹。
B: 有一社交網站(名字…你懂的),有三項動作﹕(1)X在Y的留言板上留言 (+15分) (2)X在Y的貼文內留言 (+10分) (3)X讚Y的post。你知道你名字和一系列的動作,每項動作將會替X和Y添加括號內所述的分數。問對於你來說,跟你互動而分數最多至最少的的人的排序是怎樣。即使沒跟你互動都要顯示出來。我錯了幾次是因為沒看到分數是相對於自己…
C: $Q$ 次詢問,每次問區間 $[a, b]$ 內 $\text{gcd}(X, Y)$ 最大的因數。腦殘的爆發點,明明 $O(Q\sqrt{\text{gcd}(X, Y)})$ 可以搞定,我卻寫了質素因數分解,二分找答案…當然是趕急的寫,最後也過不了…
D: 有 $N$ 個小數組,現有 $M$ 個標號,把各標號對應的數組接了起來,問其最大連續子序列和最大是多少。又一腦殘點,漏了個很容易考慮到的情況。首先對每個小數組,求出其左連接最大和,數組和,及右連接最大和。那麼對每標號則考當前和加上數組和是否單調上升。若是則加上數組和並繼續,否則應先更近答案,皆因當前數值可至少加上該標號的左連接最大和使得更大但沒法再向右繼續;之後應從甚麼數開始再繼續?答案就是數組和或右連接最大和之間的最大值。但是注意,每次輸入一個新標號之後,其小數組的最大連續子序列和可能就是唯一答案,必須同時預先比對答案和其數值。我漏了處理這個,連pretest都過不了。
E: 待補。
Codeforces #73 D FreeDiv
題意﹕給了 $N$ 個點,現在接了 $M$ 條藍色邊,一個由藍色邊接成的連通塊稱作藍色領域。現在你可以添加紅色邊使得所有藍色領域都連通起來,但是有限制﹕(1)每點只能接上最多一條紅色邊。(2)每個藍色領域不能接上超過 $k$ 條紅色邊。
根據這個限制,有可能沒法添加紅色邊使得所有藍色領域都連通起來。現問至少需添加多少條藍色邊使得能達成要求?
首先,我們若把所有藍色領域縮成一點,每點標號為 $\min(k, b_i)$ ,當中 $b_i$ 為第 $i$ 個藍色領域的點數。那麼其標號即為限制讓人藍色領域最多可外接多少條紅色邊。現在問題可看成兩種操作﹕
(1) 添加藍邊連接領域 $u$ 和 $v$ 。那麼新的點 $w$ 即可看作新的藍色領域,標號為 $\min(b_u+b_v, k)$ 。
(2) 添加紅邊連接領域 $u$ 和 $v$ 。那麼新的點 $w$ 即可看作新的藍色領域,標號為 $(b_u+b_v - 2)$ 。
假定不允許操作(1)(即添加藍色邊),甚麼時候會不能滿足問題條件?明顯是存在兩個點 $u, v$ 使得 $b_u=b_v=1$ 並只能為這兩點進行操作(2)。甚麼時候可以盡量防止這情況發生?留意當 $b_u, b_v \ge 2$ 操作(2)只會製造一個新點 $w$ 使得 $b_w \ge \max(b_u, b_v)$ ,故不會導致失敗。那麼可以先為標號從大到小排序,順著標號進行操作(2)即可,只要當中有標號少於零的即當作失敗。
如果允許操作(1),怎樣可以把操作(1)的數量最少又使得條件滿足?可用二分搜索答案。假設你只允許進行操作(1) $p$ 次,你會怎樣進行操作(1)使得用上段的方法添加紅邊後條件滿足?不難留意上段說明失敗的情況只有標號為1的點太多的時候才會發生。要避免這個情況,可以考慮每次把兩個標號為1的點用操作(1)連起來,成為一個標號為 $2$ 的點。再由上段可知,它和標號大於2的點添加紅邊,不會出現失敗情況;它杏標號為1的點添加紅邊,會變成只有一個標號為1的點。故把兩兩標號為1的點用藍邊連接最能防止失敗的情況。
我寫的時候用了STL的priority_queue,結果超時(5秒都超…)。改用STL的make_heap之後剛好4.5秒通過了…另,我認為可以不用二分,直接可以算出應最少用多少次操作(1)。
根據這個限制,有可能沒法添加紅色邊使得所有藍色領域都連通起來。現問至少需添加多少條藍色邊使得能達成要求?
首先,我們若把所有藍色領域縮成一點,每點標號為 $\min(k, b_i)$ ,當中 $b_i$ 為第 $i$ 個藍色領域的點數。那麼其標號即為限制讓人藍色領域最多可外接多少條紅色邊。現在問題可看成兩種操作﹕
(1) 添加藍邊連接領域 $u$ 和 $v$ 。那麼新的點 $w$ 即可看作新的藍色領域,標號為 $\min(b_u+b_v, k)$ 。
(2) 添加紅邊連接領域 $u$ 和 $v$ 。那麼新的點 $w$ 即可看作新的藍色領域,標號為 $(b_u+b_v - 2)$ 。
假定不允許操作(1)(即添加藍色邊),甚麼時候會不能滿足問題條件?明顯是存在兩個點 $u, v$ 使得 $b_u=b_v=1$ 並只能為這兩點進行操作(2)。甚麼時候可以盡量防止這情況發生?留意當 $b_u, b_v \ge 2$ 操作(2)只會製造一個新點 $w$ 使得 $b_w \ge \max(b_u, b_v)$ ,故不會導致失敗。那麼可以先為標號從大到小排序,順著標號進行操作(2)即可,只要當中有標號少於零的即當作失敗。
如果允許操作(1),怎樣可以把操作(1)的數量最少又使得條件滿足?可用二分搜索答案。假設你只允許進行操作(1) $p$ 次,你會怎樣進行操作(1)使得用上段的方法添加紅邊後條件滿足?不難留意上段說明失敗的情況只有標號為1的點太多的時候才會發生。要避免這個情況,可以考慮每次把兩個標號為1的點用操作(1)連起來,成為一個標號為 $2$ 的點。再由上段可知,它和標號大於2的點添加紅邊,不會出現失敗情況;它杏標號為1的點添加紅邊,會變成只有一個標號為1的點。故把兩兩標號為1的點用藍邊連接最能防止失敗的情況。
我寫的時候用了STL的priority_queue,結果超時(5秒都超…)。改用STL的make_heap之後剛好4.5秒通過了…另,我認為可以不用二分,直接可以算出應最少用多少次操作(1)。
2011年4月7日 星期四
Codeforces #62 D Wormhouse
題意﹕現有一個 $N$ 點的歐拉迴路的遍歷,這遍歷包含 $M$ 條邊。詢問字典序的下一個大的遍歷。可以不存在,圖亦可以不連通。 $3 \le N \le 100, 3 \le M \le 2000$ 。
做法是比較直接的。枚舉迴路的前綴,假設前綴的末點是 $u$ ,本來的下一遍歷點是 $v$ ,則在此刻嘗試找迴路的時候,嘗試的點應至少由 $v+1$ 開始。其餘時候則保持從最小標號點開始。然後直接比較路徑(如有)即可。
做法是比較直接的。枚舉迴路的前綴,假設前綴的末點是 $u$ ,本來的下一遍歷點是 $v$ ,則在此刻嘗試找迴路的時候,嘗試的點應至少由 $v+1$ 開始。其餘時候則保持從最小標號點開始。然後直接比較路徑(如有)即可。
2011年4月6日 星期三
Codeforces #12 D Ball
問題非常簡短﹕給了 $N$ 個三維空間的點,問有多少個點 $i$ 使得存在點 $j$ 令 $x_i < x_j, y_i < y_j, z_i < z_j$ 。 $1 \le N \le 500000$ , $0 \le x_i, y_i, z_i \le 10^9$ 。
其實做法非常經典,屬練習題程度,可是我比較笨,老是想不出正確的方法。
為 $x_i$ 排序,然後把 $y_i$ 離散化。按 $x_i$ 從大至小遍歷,則問題等價於找出 $y_i < y_j$ 並且 $z_i < z_j$ 。再把問題重新看一下則是尋找 $\max_{j: y_i < y_j}\{z_j\}$ 。因 $y_i$ 已離散化則不妨把它看成位置,現求在點 $i$ 的情況下,範圍 $j \in [y_i+1, M]$ 內 $z_j$ 的最大值,當中 $M$ 是指 $y_i$ 有多少個不同的數值(即離散化後的最大值)。如此一來即是求範圍內最大值,線段樹秒殺之。
注意題目要求的是 $x_i < x_j$ 。遍歷 $x_i$ 值從大至小的時候要把相同的 $x_i$ 值暫緩更新,否則會出錯。附一樣例作例子。
其實做法非常經典,屬練習題程度,可是我比較笨,老是想不出正確的方法。
為 $x_i$ 排序,然後把 $y_i$ 離散化。按 $x_i$ 從大至小遍歷,則問題等價於找出 $y_i < y_j$ 並且 $z_i < z_j$ 。再把問題重新看一下則是尋找 $\max_{j: y_i < y_j}\{z_j\}$ 。因 $y_i$ 已離散化則不妨把它看成位置,現求在點 $i$ 的情況下,範圍 $j \in [y_i+1, M]$ 內 $z_j$ 的最大值,當中 $M$ 是指 $y_i$ 有多少個不同的數值(即離散化後的最大值)。如此一來即是求範圍內最大值,線段樹秒殺之。
注意題目要求的是 $x_i < x_j$ 。遍歷 $x_i$ 值從大至小的時候要把相同的 $x_i$ 值暫緩更新,否則會出錯。附一樣例作例子。
3
0 0 0
0 0 1
0 0 1
2011年4月2日 星期六
Codeforces #27 D Ring Road 2
題意﹕給了一個帶 $N$ 個頂點的環 $C_N$ ,現在要添加 $M$ 條邊,你可以把邊畫在環內,或是環外,但必須使得每條邊之間都不能相交(在末端相交除外)。問是否存在一個決定邊的畫法使得條件達成。保証邊連接不同的頂點,沒重邊。
最初有一個很直觀的想法﹕假設邊是 $e = (x, y)$ 且 $x < y$ ,設 $A_e = \{i: x < i < y\}$ , $B_e = \{1 \cdots N\} - A_e - \{x, y\}$ ,則 $e$ 會把頂點集分開兩半,使得任意邊 $e' = (x', y'), x' \in A_e, y' \in B_e$ 必不能與 $e$ 有相同的畫法。我們稱 $e$ 和 $e'$ 是互斥的。
可惜之後有一個錯的想法。以為順著輸入每條邊,都更新使得互斥的點對的可用的畫法,如遇上某一點對沒有可用的畫法則判無解。這個算法是錯的,只是我未找到反例。
然後有另一個想法,就是基於兩個互斥的點對必須有不同的畫法。可以立刻聯想到的是若把點對看作一個頂點,互斥點對添加一條邊,則此構造圖 $G$ 有解若且僅若 $G$ 是二分的(即可以用兩種顏色為頂點著色)。這就是正確的解。
順帶一提,本題要求的添加邊使得解是一平面圖,但必須基於 $C_N$ 底下該圖仍是平面的。所以不用想平面圖測試的算法了。
最初有一個很直觀的想法﹕假設邊是 $e = (x, y)$ 且 $x < y$ ,設 $A_e = \{i: x < i < y\}$ , $B_e = \{1 \cdots N\} - A_e - \{x, y\}$ ,則 $e$ 會把頂點集分開兩半,使得任意邊 $e' = (x', y'), x' \in A_e, y' \in B_e$ 必不能與 $e$ 有相同的畫法。我們稱 $e$ 和 $e'$ 是互斥的。
可惜之後有一個錯的想法。以為順著輸入每條邊,都更新使得互斥的點對的可用的畫法,如遇上某一點對沒有可用的畫法則判無解。這個算法是錯的,只是我未找到反例。
然後有另一個想法,就是基於兩個互斥的點對必須有不同的畫法。可以立刻聯想到的是若把點對看作一個頂點,互斥點對添加一條邊,則此構造圖 $G$ 有解若且僅若 $G$ 是二分的(即可以用兩種顏色為頂點著色)。這就是正確的解。
順帶一提,本題要求的添加邊使得解是一平面圖,但必須基於 $C_N$ 底下該圖仍是平面的。所以不用想平面圖測試的算法了。
2011年4月1日 星期五
Codeforces #56 E Domino Principle
題意﹕給定 $N$ 個多米諾/骨牌,每個骨牌皆有不同的位置 $X_1 \cdots X_N$ 和高度 $H_1 \cdots H_N$ 。若推倒第 $i$ 個骨牌則 $X_i+1$ 至 $X_i+H_i-1$ 以內的所有骨牌皆會倒下。問每塊骨牌可推倒多少個骨牌(包括自己)。 $1 \le N \le 10^5$ , $-10^8 \le X_i \le 10^8$ 和 $2 \le H_i \le 10^8$ 。
做法當然不能 $O(N^2)$ 枚舉吧。不過先假設 $X_1 < X_2 \cdots < X_N$ ,定義要求答案為 $f_i$ 。設 $c_i = j$ 使得 $X_i + H_i - 1 \le X_j, j > i$ ,即第 $i$ 個骨牌可以接觸到最遠哪個骨牌,如果遇上任何不能推倒的骨牌則表示為 $c_i = \infty$ 。則 $f_i$ 有如下關係﹕
\[ f_i = \begin{cases} \max_{i+1\le k\le c_i}\{f_k + k - i\} & \text{if } c_i \ne \infty \\ 1 & \text{otherwise} \end{cases}\]
首先,對於任意 $i$ ,查找 $c_i$ 的方法可以用二分搜索。至於計算 $f_i$ ,我們考慮 $c_i \ne \infty$ 的情況。經簡化可得
\[ f_i = \max_{i+1\le k\le c_i}\{f_k + k - i\} = \max_{i+1\le k\le c_i}\{f_k + k\} - i\]
設 $g_k = f_k + k$ 。即,我們從範圍 $i+1$ 至 $c_i$ 之間搜索最大的 $g_k$ 值,這就可以用線段樹輕鬆搞定了。算好 $f_i = \max_k\{g_k\} - i$ 後記得為線段樹的區間 $[i, i]$ 插入數值 $g_i = f_i + i$ 。
說來湊巧,最近與Gagguy聊天起他提起類似問題的做法,之後再做題就剛好遇上此題,所以推導公式還是比較便捷,在此先行感謝Gagguy指點。
做法當然不能 $O(N^2)$ 枚舉吧。不過先假設 $X_1 < X_2 \cdots < X_N$ ,定義要求答案為 $f_i$ 。設 $c_i = j$ 使得 $X_i + H_i - 1 \le X_j, j > i$ ,即第 $i$ 個骨牌可以接觸到最遠哪個骨牌,如果遇上任何不能推倒的骨牌則表示為 $c_i = \infty$ 。則 $f_i$ 有如下關係﹕
\[ f_i = \begin{cases} \max_{i+1\le k\le c_i}\{f_k + k - i\} & \text{if } c_i \ne \infty \\ 1 & \text{otherwise} \end{cases}\]
首先,對於任意 $i$ ,查找 $c_i$ 的方法可以用二分搜索。至於計算 $f_i$ ,我們考慮 $c_i \ne \infty$ 的情況。經簡化可得
\[ f_i = \max_{i+1\le k\le c_i}\{f_k + k - i\} = \max_{i+1\le k\le c_i}\{f_k + k\} - i\]
設 $g_k = f_k + k$ 。即,我們從範圍 $i+1$ 至 $c_i$ 之間搜索最大的 $g_k$ 值,這就可以用線段樹輕鬆搞定了。算好 $f_i = \max_k\{g_k\} - i$ 後記得為線段樹的區間 $[i, i]$ 插入數值 $g_i = f_i + i$ 。
說來湊巧,最近與Gagguy聊天起他提起類似問題的做法,之後再做題就剛好遇上此題,所以推導公式還是比較便捷,在此先行感謝Gagguy指點。
2011年3月30日 星期三
SRM 501 Div 1 Easy + Medium
剛好這次SRM撞在吃飯的時間,沒打。不過題目是清一色動態規劃,則有點兒那個…
Easy: 一開始計數器 $C$ 置0。你可以做兩種操作。操作A: $C := C + P_A$ ;操作B﹕ $C := C\times P_B$ 。你只可以使用兩種操作分別為 $N_A$ 和 $N_B$ 次,操作可按任意順序,問最大值可以是多少? 注意 $P_A$ 和 $P_B$ 皆可以是負數(不然你早就知道答案是 $C_{\max} = N_AP_AP_B^{N_B}$ )。
秒殺類動態規劃。設 $F_{\max}(i, j)$ 和 $F_{\min}(i, j)$ 為經過 $i$ 次操作A和 $j$ 次操作B之後得到的最大及最小值。除基本情況下狀態轉移方程則是
\[F_{\max}(i, j) = \max\{F_{\min}(i-1, j), F_{\max}(i-1, j), F_{\min}(i, j-1), F_{\max}(i, j-1)\}+ P_A\]
\[F_{\min}(i, j) = \min\{F_{\min}(i-1, j), F_{\max}(i-1, j), F_{\min}(i, j-1), F_{\max}(i, j-1)\}\times P_B\]
$O(N_AN_B)$ 的就是做。
另外,留意到我說全部都是正數的情況嗎?其實另有一個挺簡單的算法。
假設 $S_A = N_AP_A$ ,我們則只需取 $\max_{0 \le i \le N_B}\{S_A \times P_B^i\}$ 即可。
原因是很簡單的,我們可以真的不用乘 $P_B$ 剛好 $N_B$ 次,如果想乘剛好 $k$ 次的話,餘下的 $N_B-k$ 次則可以先在 $C = 0$ 的時候用 $N_B - k$ 次操作B抵銷掉。至於為何這種模式的操作次序為何保証答案最優,則可以考慮情況再作分析即可。
Medium: 一個 $N$ 個元素的數列 $A$ 是美麗的數列,若且僅若以下條件成立﹕
給定的數列的能帶-1。現在問,如果為這些帶-1的元素取代成0至40之間的整數,問有多少個構成的數列是美麗的數列?答案取模 $10^9+7$ 。
又是動態規劃題。今次的狀態是這樣定義的﹕ $F(i, v, d, s)$ 。 $i$ 是指當前第幾個元素, $v$ 是指當前第 $i-1$ 個元素是甚麼, $d$ 是指 $v$ 是第幾個嚴格遞降元素, $s$ 是指 $s = \sum_{j=1}^{i-1}A_j$ 。那麼可以轉移的合法狀態是甚麼呢?設能轉移的合法狀態是 $F(i+1, v', d', s')$ 。則有
只要按這些參數枚舉,則可以把所有合法的 $F(i+1, v', d', s')$ 更新成 $F(i+1, v', d', s') := F(i+1, v', d', s') + F(i, v, d, s) $ 。最底層則是 $F(0, 0, 0, 0) = 1$ 。可以根據上述的條件限制一定的枚舉範圍避免超時。答案就是 $\sum_{v, d, s} F(N, v, d, s) \bmod{10^9+7}$ 。
Easy: 一開始計數器 $C$ 置0。你可以做兩種操作。操作A: $C := C + P_A$ ;操作B﹕ $C := C\times P_B$ 。你只可以使用兩種操作分別為 $N_A$ 和 $N_B$ 次,操作可按任意順序,問最大值可以是多少? 注意 $P_A$ 和 $P_B$ 皆可以是負數(不然你早就知道答案是 $C_{\max} = N_AP_AP_B^{N_B}$ )。
秒殺類動態規劃。設 $F_{\max}(i, j)$ 和 $F_{\min}(i, j)$ 為經過 $i$ 次操作A和 $j$ 次操作B之後得到的最大及最小值。除基本情況下狀態轉移方程則是
\[F_{\min}(i, j) = \min\{F_{\min}(i-1, j), F_{\max}(i-1, j), F_{\min}(i, j-1), F_{\max}(i, j-1)\}\times P_B\]
$O(N_AN_B)$ 的就是做。
另外,留意到我說全部都是正數的情況嗎?其實另有一個挺簡單的算法。
假設 $S_A = N_AP_A$ ,我們則只需取 $\max_{0 \le i \le N_B}\{S_A \times P_B^i\}$ 即可。
原因是很簡單的,我們可以真的不用乘 $P_B$ 剛好 $N_B$ 次,如果想乘剛好 $k$ 次的話,餘下的 $N_B-k$ 次則可以先在 $C = 0$ 的時候用 $N_B - k$ 次操作B抵銷掉。至於為何這種模式的操作次序為何保証答案最優,則可以考慮情況再作分析即可。
Medium: 一個 $N$ 個元素的數列 $A$ 是美麗的數列,若且僅若以下條件成立﹕
- $A_i \le \frac{\sum_{j=1}^{i-1}A_j}{i-1}, i > 1$
- 沒有連續三個元素使得 $A_{i-1} > A_i > A_{i+1}$
- $0 \le A_i \le 40$
給定的數列的能帶-1。現在問,如果為這些帶-1的元素取代成0至40之間的整數,問有多少個構成的數列是美麗的數列?答案取模 $10^9+7$ 。
又是動態規劃題。今次的狀態是這樣定義的﹕ $F(i, v, d, s)$ 。 $i$ 是指當前第幾個元素, $v$ 是指當前第 $i-1$ 個元素是甚麼, $d$ 是指 $v$ 是第幾個嚴格遞降元素, $s$ 是指 $s = \sum_{j=1}^{i-1}A_j$ 。那麼可以轉移的合法狀態是甚麼呢?設能轉移的合法狀態是 $F(i+1, v', d', s')$ 。則有
- $0 \le v' \le 40$
- $d' = \begin{cases} 0 & \text{ if } v' \ge v \\ d+1 & \text{ otherwise } \end{cases}$ 而且 $d' \ne 2$
- $s' = s + v'$
- $i\times v' \le s $
只要按這些參數枚舉,則可以把所有合法的 $F(i+1, v', d', s')$ 更新成 $F(i+1, v', d', s') := F(i+1, v', d', s') + F(i, v, d, s) $ 。最底層則是 $F(0, 0, 0, 0) = 1$ 。可以根據上述的條件限制一定的枚舉範圍避免超時。答案就是 $\sum_{v, d, s} F(N, v, d, s) \bmod{10^9+7}$ 。
2011年3月29日 星期二
Codeforces #71
趕paper的關係,加上不知道三天前莫斯科時區改變了,所以沒有註冊。不過挺好的,以後CFBR都提早一小時,省得要兩三時才捨得去睡。
A: 給出長度為 $N$ 的字串 $S$ ,只有當 $N > 10$ 的時候把除首尾字元外移去並寫成其移去的長度,即 $N-2$ 。有做軟件開發的應該聽過 internationalization => i18n 這回事吧。秒殺題。
B: 一個顯示進度的顯示塊,分成 $N$ 等分。 每等份的顏色深度最多為 $K$ 。現在問進度為 $0 \le t \le 100$ 的情況下每個進度顯示塊的顏色深度是多少。設進度塊的顏色深度是 $a_1 \le a_2 \le \cdots \le a_N$ ,則必需滿足
\[\frac{\sum_i a_i}{NK} \le t < \frac{\sum_i a_i + 1}{NK}\]
只需枚舉 $\sum_{i} a_i$ 的值即可。注意別忘記該值最多可以是 $NK$ 。
C: 問在一圓形上均勻分佈 $N$ 點,每點可以是紅色或綠色,問有沒有在一綠色連成正 $K \ge 3$ 邊形。直接想法就是給定一正 $N$ 邊形結構,只能構造正 $k$ 邊形若且僅若 $k | N$ 。因此枚舉 $N$ 的因數然後直接查找有無正 $K$ 邊形即可。一個 $m | N$ 相隔的點連通可以構造成 $\frac{N}{m}$ 邊形。注意不可枚舉 $\frac{N}{m} \le 2$ 的情況(考慮 $N = 4$ )。
D: 給了 $N \times M$ 張樸克牌,當中有至多兩隻鬼牌,你可以把鬼牌任意換成輸入的樸克牌中沒有的牌,但牌沒有重複。問有否存在兩個互不重疊的 $3 \times 3$ 的正方形,每個必須覆蓋其中9張牌,使得每個正方形所覆蓋的牌中,必須保証同花或者數字互不相同。然後按題目描述輸出。
好麻煩的數據處理題。總之寫得小心點即可。留意如果只有一張J2牌不要誤輸出為J1牌,有兩張鬼牌的話需要搞清次序。
E: 題目是給了 $N$ 個整數 $A_1, \cdots A_N$ ,每個不太於100。問能否通過劃分並取和後得出另外給定的 $K$ 個整數 $B_1, \cdots B_K$ ,同樣的,每個不多於100。數據範圍是 $1 \le K \le N \le 17$ 。如果能找到解必須輸出如何劃分,為使題目變得更「有趣」,出題者把數字變成化學元素,取和就是進行核融合(這真是抽了日本一把)。
我的做法是動態規劃。記 $f_{b, k}$ ,當前劃分過的數字以一集合 $b$ 表示,並且它們都可以表達了首 $k$ 個數,而 $f_{b, k}$ 僅表示這個情況能否實現,1代表能夠,0則代表不能。轉移方程則是
\[f_{b, k} = \bigvee_{b': b' \subseteq b\text{ and }s_{b-b'}=B_k} f_{b', k-1} \]
\[f_{\emptyset, 0} = 1,\quad f_{\emptyset, k} = 0 \text{ for }k > 0\]
其中
\[s_b = \sum_{i \in b} A_i\]
可預先用 $O(n2^n)$ 動態規劃計算。
麻煩的是計算 $f_{b, k}$ 的運算量最壞可以是 $O(n2^{2n})$ 。
我用了一點優化的技巧還是過了。首先,對於 $f_{b, k}$ 的計算,只需要預計算所有 $s_{b-b'}=B_k$ 即可,無需所有集合都試一次。另外,計算 $f_{\cdot, k}$ 的時候已有哪些 $b$ 使得 $f_{b, k}$ 是可行的,假設集合 $S'$ 包含這些子集 $b$ 。下次計算 $f_{\cdot, k+1}$ 時則只需從集合 $S$ 內的子集取 $f_{b, k}$ 計算即可。通過這種優化則可以在最遲2.5秒左右跑完數據。
A: 給出長度為 $N$ 的字串 $S$ ,只有當 $N > 10$ 的時候把除首尾字元外移去並寫成其移去的長度,即 $N-2$ 。有做軟件開發的應該聽過 internationalization => i18n 這回事吧。秒殺題。
B: 一個顯示進度的顯示塊,分成 $N$ 等分。 每等份的顏色深度最多為 $K$ 。現在問進度為 $0 \le t \le 100$ 的情況下每個進度顯示塊的顏色深度是多少。設進度塊的顏色深度是 $a_1 \le a_2 \le \cdots \le a_N$ ,則必需滿足
只需枚舉 $\sum_{i} a_i$ 的值即可。注意別忘記該值最多可以是 $NK$ 。
C: 問在一圓形上均勻分佈 $N$ 點,每點可以是紅色或綠色,問有沒有在一綠色連成正 $K \ge 3$ 邊形。直接想法就是給定一正 $N$ 邊形結構,只能構造正 $k$ 邊形若且僅若 $k | N$ 。因此枚舉 $N$ 的因數然後直接查找有無正 $K$ 邊形即可。一個 $m | N$ 相隔的點連通可以構造成 $\frac{N}{m}$ 邊形。注意不可枚舉 $\frac{N}{m} \le 2$ 的情況(考慮 $N = 4$ )。
D: 給了 $N \times M$ 張樸克牌,當中有至多兩隻鬼牌,你可以把鬼牌任意換成輸入的樸克牌中沒有的牌,但牌沒有重複。問有否存在兩個互不重疊的 $3 \times 3$ 的正方形,每個必須覆蓋其中9張牌,使得每個正方形所覆蓋的牌中,必須保証同花或者數字互不相同。然後按題目描述輸出。
好麻煩的數據處理題。總之寫得小心點即可。留意如果只有一張J2牌不要誤輸出為J1牌,有兩張鬼牌的話需要搞清次序。
E: 題目是給了 $N$ 個整數 $A_1, \cdots A_N$ ,每個不太於100。問能否通過劃分並取和後得出另外給定的 $K$ 個整數 $B_1, \cdots B_K$ ,同樣的,每個不多於100。數據範圍是 $1 \le K \le N \le 17$ 。如果能找到解必須輸出如何劃分,為使題目變得更「有趣」,出題者把數字變成化學元素,取和就是進行核融合(這真是抽了日本一把)。
我的做法是動態規劃。記 $f_{b, k}$ ,當前劃分過的數字以一集合 $b$ 表示,並且它們都可以表達了首 $k$ 個數,而 $f_{b, k}$ 僅表示這個情況能否實現,1代表能夠,0則代表不能。轉移方程則是
\[f_{\emptyset, 0} = 1,\quad f_{\emptyset, k} = 0 \text{ for }k > 0\]
其中
可預先用 $O(n2^n)$ 動態規劃計算。
麻煩的是計算 $f_{b, k}$ 的運算量最壞可以是 $O(n2^{2n})$ 。
我用了一點優化的技巧還是過了。首先,對於 $f_{b, k}$ 的計算,只需要預計算所有 $s_{b-b'}=B_k$ 即可,無需所有集合都試一次。另外,計算 $f_{\cdot, k}$ 的時候已有哪些 $b$ 使得 $f_{b, k}$ 是可行的,假設集合 $S'$ 包含這些子集 $b$ 。下次計算 $f_{\cdot, k+1}$ 時則只需從集合 $S$ 內的子集取 $f_{b, k}$ 計算即可。通過這種優化則可以在最遲2.5秒左右跑完數據。
2011年3月27日 星期日
Codeforces #70 C Lucky Tickets
題意﹕若有一對數 $(p, q)$ 使得 $p\times q = \hat{p} \times \hat{q}$ ,當中 $\hat{x}$ 是指把 $x$ 的十進制倒置並消去前導零,我們則稱 $(p, q)$ 為幸運對。給定 $X_{\max}, Y_{\max}$ ,求一 $x, y$ 對使得對於任意 $1 \le i \le x,\quad 1 \le j \le y$ , $(i, j)$ 是幸運對的數量至少為 $w$ 。求最小的 $x\times y$ 使得條件成立。
首先需要注意的是若 $(p, q)$ 是一幸運對的話,則有如下公式
\[\frac{p}{\hat{p}} = \frac{\hat{q}}{q}\]
另,只要任意 $p'$ 使得 $\dfrac{p}{\hat{p}} = \dfrac{p'}{\hat{p'}}$ ,則 $(p', q)$ 也是幸運對。因此我們先要留意把 $\dfrac{p}{\hat{p}}$ 化至最簡。設 $\acute{p}$ 和 $\grave{q}$ 為 $\dfrac{p}{\hat{p}}$ 和 $\dfrac{\hat{q}}{q}$ 的最簡化分數,若 $C_{\acute{p}}$ 和 $D_{\grave{q}}$ 分別包含所有 $i$ 使得 $\acute{i} = \acute{p}$ 和 $j$ 使得 $\grave{j} = \grave{q}$ ,則對於任意的 $i \in C_{\acute{p}}$ 和 $j\in D_{\grave{q}}$ , $(i, j)$ 必為幸運對,而且一共有 $|C_{\acute{p}}||D_{\grave{q}}|$ 個。
因此先計算所有 $|C_x|$ 的值。這個可以在 $O(X_{\max}\log X_{\max})$ 時間內完成。然後先從 $x = X_{\max}, y=1$ 開始,在不斷減少 $x$ 的同時,提升 $y$ 使得總幸運對至少為 $w$ 。留意每增加一次 $y$ ,便會相應增加了 $|C_{\grave{y}}|$ 組幸運對。並且同一時間統計 $D_{\grave{y}}$ 。當再增加 $|C_{\grave{y}}|$ 組幸運對時超過了 $w$ 則停止統計,並更新答案。這個時候已知再增加 $y$ 不會令答案變得更好,因此可以考慮減少 $x$ 。但減少了 $x$ 將會對原本計算現有多少組幸運對有影響。 $x$ 自身可以和 $|D_{\acute{x}}|$ 個數組成幸運對,因此當 $x$ 減少了一的時候,相應的幸運對的數量須減少$|D_{\acute{x}}|$ ,同時為 $C_{\acute{x}}$ 移去 $x$ 。
這個算法可以在 $O((X_{\max} + Y_{\max})(\log X_{\max}Y_{\max}))$ 時間內完成。
首先需要注意的是若 $(p, q)$ 是一幸運對的話,則有如下公式
\[\frac{p}{\hat{p}} = \frac{\hat{q}}{q}\]
另,只要任意 $p'$ 使得 $\dfrac{p}{\hat{p}} = \dfrac{p'}{\hat{p'}}$ ,則 $(p', q)$ 也是幸運對。因此我們先要留意把 $\dfrac{p}{\hat{p}}$ 化至最簡。設 $\acute{p}$ 和 $\grave{q}$ 為 $\dfrac{p}{\hat{p}}$ 和 $\dfrac{\hat{q}}{q}$ 的最簡化分數,若 $C_{\acute{p}}$ 和 $D_{\grave{q}}$ 分別包含所有 $i$ 使得 $\acute{i} = \acute{p}$ 和 $j$ 使得 $\grave{j} = \grave{q}$ ,則對於任意的 $i \in C_{\acute{p}}$ 和 $j\in D_{\grave{q}}$ , $(i, j)$ 必為幸運對,而且一共有 $|C_{\acute{p}}||D_{\grave{q}}|$ 個。
因此先計算所有 $|C_x|$ 的值。這個可以在 $O(X_{\max}\log X_{\max})$ 時間內完成。然後先從 $x = X_{\max}, y=1$ 開始,在不斷減少 $x$ 的同時,提升 $y$ 使得總幸運對至少為 $w$ 。留意每增加一次 $y$ ,便會相應增加了 $|C_{\grave{y}}|$ 組幸運對。並且同一時間統計 $D_{\grave{y}}$ 。當再增加 $|C_{\grave{y}}|$ 組幸運對時超過了 $w$ 則停止統計,並更新答案。這個時候已知再增加 $y$ 不會令答案變得更好,因此可以考慮減少 $x$ 。但減少了 $x$ 將會對原本計算現有多少組幸運對有影響。 $x$ 自身可以和 $|D_{\acute{x}}|$ 個數組成幸運對,因此當 $x$ 減少了一的時候,相應的幸運對的數量須減少$|D_{\acute{x}}|$ ,同時為 $C_{\acute{x}}$ 移去 $x$ 。
這個算法可以在 $O((X_{\max} + Y_{\max})(\log X_{\max}Y_{\max}))$ 時間內完成。
2011年3月26日 星期六
Codeforces #54 D Writing a Song
題意﹕給定 $N$ 和 $K$ ,現在有一長度為 $L_P$ 的字串 $P$ 和一長度為 $N - L_P + 1$ 的01字串 $B$ ,並依 $B$ 構造一長度為 $N$ 的字串 $R$ 。若 $B_i$ 為1,則子字串 $R_{i\cdots i+L_P-1}$ 必須要等於字串 $P$ 。若 $B_i$ 為0則該子字串必須不能等於 $P$ 。另,只能使用首 $K$ 個小寫英文字母。問能否存在此字串並輸出答案。
顯然易見的是某些位置該於甚麼字元是固定的。先把那些地方寫好固定的字元。然後檢測有否沖突。如果有衝突的話則必無解。
但,如無衝突的話,可能存在未固定字元的位置,那麼該放甚麼呢?首先理解的是不能亂放。可以參考題中第二樣例。
如果允許字元只有 $\{a, b\}$ 而且 $P = a$ 、 $B = \underbrace{10\cdots 01}_{N-2\text{ zeros}}$ 。那麼除固定首尾為a之外,其餘位置必須放置b。如果隨機放的話,只有 $\frac{1}{2^{N-2}}$ 機會判斷正確。那麼,當 $N$ 很大的時候幾乎沒有可能找到正確(且唯一的)解。那麼是不是代表亂放不奏效?又未必!
其實大可以想想以下一個有可能錯的算法﹕對於未固定位置,枚舉可放置的字元,找到第一個能放的字元又不引起衝突即可。這個算法,相信大家很快找到反例﹕某一個位置首先找到的字元,可能會令往後的任意放置變成無解。於是,先放置甚麼字元就顯得比較重要了。來到這裡,可以問一個問題了﹕能不能應用隨機算法?似乎可行。每次枚舉未固定位置前,先為可用字元隨機取一排列 $\sigma$ ,然後按 $\sigma$ 的順序嘗試。把這個過程重複 $T$ 次,估計誤判沒有解的機會很小。我的算法甚至取 $T = 1$ 都可以安然通過。
至於為甚麼能找到解的機會很高?這個我沒法証明…
另,正確的解法是動態規劃。
顯然易見的是某些位置該於甚麼字元是固定的。先把那些地方寫好固定的字元。然後檢測有否沖突。如果有衝突的話則必無解。
但,如無衝突的話,可能存在未固定字元的位置,那麼該放甚麼呢?首先理解的是不能亂放。可以參考題中第二樣例。
如果允許字元只有 $\{a, b\}$ 而且 $P = a$ 、 $B = \underbrace{10\cdots 01}_{N-2\text{ zeros}}$ 。那麼除固定首尾為a之外,其餘位置必須放置b。如果隨機放的話,只有 $\frac{1}{2^{N-2}}$ 機會判斷正確。那麼,當 $N$ 很大的時候幾乎沒有可能找到正確(且唯一的)解。那麼是不是代表亂放不奏效?又未必!
其實大可以想想以下一個有可能錯的算法﹕對於未固定位置,枚舉可放置的字元,找到第一個能放的字元又不引起衝突即可。這個算法,相信大家很快找到反例﹕某一個位置首先找到的字元,可能會令往後的任意放置變成無解。於是,先放置甚麼字元就顯得比較重要了。來到這裡,可以問一個問題了﹕能不能應用隨機算法?似乎可行。每次枚舉未固定位置前,先為可用字元隨機取一排列 $\sigma$ ,然後按 $\sigma$ 的順序嘗試。把這個過程重複 $T$ 次,估計誤判沒有解的機會很小。我的算法甚至取 $T = 1$ 都可以安然通過。
至於為甚麼能找到解的機會很高?這個我沒法証明…
另,正確的解法是動態規劃。
2011年3月24日 星期四
Codeforces #23 C Oranges and Apples
題意﹕給了$2N-1$個箱子,每個箱子分別載有 $A_i$ 和 $O_i$ 個蘋果和橙。要求選出 $N$ 個箱子使得蘋果和橙的總數至少為總數的一半。 $A_i, O_i \ge 0$ 。
設蘋果和橙的總數為 $A$ 和 $O$。換句話說,就是求一集合 $\mathcal{I}\subseteq \{1\cdots 2N-1\},\, |\mathcal{I}| = N$ 使得
\[\sum_{i\in\mathcal{I}}A_i \ge \frac{A}{2},\quad \sum_{i\in\mathcal{I}}O_i \ge \frac{O}{2}\]
我的做法比較不確定,就是任意隨機取一排列 $\sigma$ 使得首 $N$ 個箱子符合條件。
正確的做法應該是這樣。不失一般性下假設
$A_1 \le A_2 \cdots \le A_{2N-1}$
把奇數項設為 $Q$ ,偶數項設為 $P$ ,則有
$Q_1 \le P_1 \le Q_2 \le P_2 \cdots P_{N-1} \le Q_N $
定理 1﹕ $\sum_i Q_i \ge \frac{A}{2}, \sum_i P_i + Q_N \ge \frac{A}{2}$ 。
對於 $ 1 \le i \le N-1$ , 皆有 $Q_{i+1} - P_i \ge 0$ 。因此 $Q_1+\sum_{i=1}^{N-1}Q_{i+1}-P_i \ge 0$ ,故 $\sum_i Q_i$ 至少為 $A$ 的一半。
另外,對於 $ 1 \le i \le N-1$ 則有 $P_i-Q_i \ge 0$ 。因此 $Q_N+\sum_{i=1}^{N-1}P_i-Q_i \ge 0$ ,故 $Q_N + \sum_i P_i$ 至少為 $A$ 的一半。
因此,把箱子依數量排序則有兩種取法使得其蘋果數的總和至少為 $A$ 的一半,而且它們皆取了第 $2N-1$ 個箱子。那麼這兩種取法的橙的數量分別有 $X = \sum_{i=1}^{N} O_{2i-1}$ 和 $Y = \sum_{i=1}^{N-1} O_{2i}+O_{2N-1}$ 。
設 $Z = Y - O_{2N-1}$ 。因為 $X + Z = O$ 。若 $X < \frac{O}{2}$ 則有 $Z \ge \frac{O}{2}$ ,反之亦然。而 $Y \ge Z$ ,因此在結論中可把 $Z$ 替換成 $Y$ 。因此按這個方法去選取箱子則保証答案永遠存在。
設蘋果和橙的總數為 $A$ 和 $O$。換句話說,就是求一集合 $\mathcal{I}\subseteq \{1\cdots 2N-1\},\, |\mathcal{I}| = N$ 使得
我的做法比較不確定,就是任意隨機取一排列 $\sigma$ 使得首 $N$ 個箱子符合條件。
正確的做法應該是這樣。不失一般性下假設
把奇數項設為 $Q$ ,偶數項設為 $P$ ,則有
定理 1﹕ $\sum_i Q_i \ge \frac{A}{2}, \sum_i P_i + Q_N \ge \frac{A}{2}$ 。
對於 $ 1 \le i \le N-1$ , 皆有 $Q_{i+1} - P_i \ge 0$ 。因此 $Q_1+\sum_{i=1}^{N-1}Q_{i+1}-P_i \ge 0$ ,故 $\sum_i Q_i$ 至少為 $A$ 的一半。
另外,對於 $ 1 \le i \le N-1$ 則有 $P_i-Q_i \ge 0$ 。因此 $Q_N+\sum_{i=1}^{N-1}P_i-Q_i \ge 0$ ,故 $Q_N + \sum_i P_i$ 至少為 $A$ 的一半。
因此,把箱子依數量排序則有兩種取法使得其蘋果數的總和至少為 $A$ 的一半,而且它們皆取了第 $2N-1$ 個箱子。那麼這兩種取法的橙的數量分別有 $X = \sum_{i=1}^{N} O_{2i-1}$ 和 $Y = \sum_{i=1}^{N-1} O_{2i}+O_{2N-1}$ 。
設 $Z = Y - O_{2N-1}$ 。因為 $X + Z = O$ 。若 $X < \frac{O}{2}$ 則有 $Z \ge \frac{O}{2}$ ,反之亦然。而 $Y \ge Z$ ,因此在結論中可把 $Z$ 替換成 $Y$ 。因此按這個方法去選取箱子則保証答案永遠存在。
Codeforces #69
題目不太難,只是有些題目比較難讀懂,遲開始了,最後得分比較低。
A: 在三維空間的原點上有一物件。應用了 次矢量為
次矢量為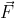 的力後,問最終物件是否原地不動。
的力後,問最終物件是否原地不動。
答案﹕檢查 $\sum_i\vec{F_i} = \vec{0}$ 即可。
B: 一條長度為 的跑道上有
的跑道上有 個section。每個跑手會在
個section。每個跑手會在 個section進行賽跑。假設個section每次賽跑都是分開進行的,若在某section裡下注了第
個section進行賽跑。假設個section每次賽跑都是分開進行的,若在某section裡下注了第 跑手贏出而真的贏出的話,則得到
跑手贏出而真的贏出的話,則得到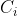 元。每人每section賽跑時間都是
元。每人每section賽跑時間都是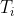 。不能在沒人跑的賽道中下注,不能在沒有某參賽者不賽跑的section向其下注,問最多可以贏到多少錢?
。不能在沒人跑的賽道中下注,不能在沒有某參賽者不賽跑的section向其下注,問最多可以贏到多少錢?
好煩的題目。但只是直接枚舉每個section,在有人跑的回報裡取最大值,然後總和就是答案。
C: 給了 種神器的原材料名稱,和
種神器的原材料名稱,和 種神器所需要的原材料及其數量。現在有
種神器所需要的原材料及其數量。現在有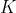 個玩家和
個玩家和 次採購。每次採購皆說明是哪位玩家買了甚麼原材料。
次採購。每次採購皆說明是哪位玩家買了甚麼原材料。
保証每次採購後只會有最多一種合作神器可以作成,問最後每人手上每種神器的數量,和有多少種神器。
直接就是做,比賽時沒過是因為我以為輸出的是玩家名稱,而不是神器的數量…
D: 在某座標) 上放了一隻棋子。兩個玩家輪流玩遊戲。每次可選取
上放了一隻棋子。兩個玩家輪流玩遊戲。每次可選取 個之中的一個矢量
個之中的一個矢量 然後加到該棋子上,保証矢量非零並且數值非負。除移動外,另可以選擇應用反射,即
然後加到該棋子上,保証矢量非零並且數值非負。除移動外,另可以選擇應用反射,即%20\rightarrow%20(y,%20x)) ,但每位玩家只能在遊戲中應用一次。玩家不能把棋子移離原點距離
,但每位玩家只能在遊戲中應用一次。玩家不能把棋子移離原點距離 以外。問若兩個玩家皆采取最佳策略,問誰會勝出。
以外。問若兩個玩家皆采取最佳策略,問誰會勝出。
經典的動態規劃題。但可以留意反射是沒有作用的,因為對方可以再應用一次反射抵銷。
另可以用SG定理,注意需處理SG函數為0的位置。
E: 給定一數組 和
和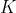 ,詢問對於
,詢問對於 ,
, 之間出現僅一次的元素的最大值,不存在的話則輸出"Nothing"。
之間出現僅一次的元素的最大值,不存在的話則輸出"Nothing"。
直接的單調隊列題。大部分選手都用STL的set,我則用了Priority Queue來做,幸好沒有超時。主要做法是當需要處理新的元素時,把最舊的元素統計減1,然後把新元素的統計加1,若是新出現的元素則放到隊列內。每次輸出時把第一個隊列置頂的元素輸出,且其需要符合統計數為1。若不合資格則把它移除。
A: 在三維空間的原點上有一物件。應用了
答案﹕檢查 $\sum_i\vec{F_i} = \vec{0}$ 即可。
B: 一條長度為
好煩的題目。但只是直接枚舉每個section,在有人跑的回報裡取最大值,然後總和就是答案。
C: 給了
保証每次採購後只會有最多一種合作神器可以作成,問最後每人手上每種神器的數量,和有多少種神器。
直接就是做,比賽時沒過是因為我以為輸出的是玩家名稱,而不是神器的數量…
D: 在某座標
經典的動態規劃題。但可以留意反射是沒有作用的,因為對方可以再應用一次反射抵銷。
另可以用SG定理,注意需處理SG函數為0的位置。
E: 給定一數組
直接的單調隊列題。大部分選手都用STL的set,我則用了Priority Queue來做,幸好沒有超時。主要做法是當需要處理新的元素時,把最舊的元素統計減1,然後把新元素的統計加1,若是新出現的元素則放到隊列內。每次輸出時把第一個隊列置頂的元素輸出,且其需要符合統計數為1。若不合資格則把它移除。
2011年3月19日 星期六
Codeforces #68
比賽題目較為簡單,但是仍然表現得不夠好。
A: 問給了4個互相不同的數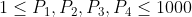 ,給了範圍
,給了範圍 ,問當中有多少個數,使得在至少7種
,問當中有多少個數,使得在至少7種 的不同排列中,該數在取模的順序下仍然保持不變。看了之後都不用懷疑,直接就
的不同排列中,該數在取模的順序下仍然保持不變。看了之後都不用懷疑,直接就 暴搞了。但留意一下取模順序本來就是符合交換性的,即
暴搞了。但留意一下取模順序本來就是符合交換性的,即\bmod{b}=(x\bmod{b})\bmod{a}) ,因此只需對一種排列(例如輸入中的排列)下試了所有數看看是否在取模順序下不變即可。省卻了24!的排列。
,因此只需對一種排列(例如輸入中的排列)下試了所有數看看是否在取模順序下不變即可。省卻了24!的排列。
然而,本題有) 的算法。假設
的算法。假設 ,可知保持取模下不變的數只能在
,可知保持取模下不變的數只能在 ,即,其餘取模是多餘的。因此答案即是
,即,其餘取模是多餘的。因此答案即是-a+1)) 。
。
B: 給定 個整數
個整數 ,定義操作
,定義操作, i\ne j, 0 \le k \le 99, x \in \mathbb{R}, 0 < x \le A_i) ,使得操作後
,使得操作後 。給定
。給定 ,問經過若干次操作後,能使得
,問經過若干次操作後,能使得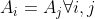 的話,它們的數值最多為多少。
的話,它們的數值最多為多少。
直接的想法就是二分答案。設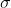 為經過若干次操作後最終每個數的一致值,定義
為經過若干次操作後最終每個數的一致值,定義
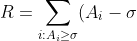, S = \sum_{i : A_i < \sigma}(\sigma-A_i)\frac{100}{100-k})
不難看出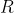 是總供給量,
是總供給量, 是總需求量。若
是總需求量。若 則表示經過若干次操作後所有數皆等於
則表示經過若干次操作後所有數皆等於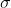 。若
。若 則表示供過於求,即
則表示供過於求,即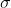 太低;若
太低;若 則表示供不應求,即
則表示供不應求,即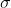 太高。應用二分法求最大的
太高。應用二分法求最大的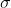 使得供求相符即可。
使得供求相符即可。
C: 給了一個有向無環圖,最多6個頂點,而且是完全圖。每條邊有要求流量最少最多值,和啟動值。設在邊) 流量是
流量是 ,啟動值
,啟動值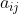 ,則費用是
,則費用是 。求一個可行的網絡流,源是點1,匯是點
。求一個可行的網絡流,源是點1,匯是點 ,需要符合上下限,要求流量最小,其次則要求費用最大。上下限最多是5,啟動費用最多是6。若沒有流量則毋需計算啟動費用。
,需要符合上下限,要求流量最小,其次則要求費用最大。上下限最多是5,啟動費用最多是6。若沒有流量則毋需計算啟動費用。
明顯地數據範圍極小,可以考慮暴試。設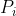 為第
為第 點的注入量。對源點則有
點的注入量。對源點則有 。DFS狀態為
。DFS狀態為) ,當中
,當中 。此程序會嘗試從點
。此程序會嘗試從點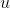 抽取
抽取) 之間的注入量,加到
之間的注入量,加到 之中,然後按情況嘗試
之中,然後按情況嘗試, f(v+1, 1)) 。當達到
。當達到) 即可中止。但嘗試量最多是
即可中止。但嘗試量最多是}{2}}) ,肯定會超時。要應用一些prunning技巧。首先,當在狀態
,肯定會超時。要應用一些prunning技巧。首先,當在狀態) 的時候,若
的時候,若 已經大於最小流量值則中止嘗試。另,嘗試
已經大於最小流量值則中止嘗試。另,嘗試) 的時候,應直接取走其注入量,並留意是否
的時候,應直接取走其注入量,並留意是否 ,若否則中止搜索。
,若否則中止搜索。
D: 待補。
A: 問給了4個互相不同的數
然而,本題有
B: 給定
直接的想法就是二分答案。設
不難看出
C: 給了一個有向無環圖,最多6個頂點,而且是完全圖。每條邊有要求流量最少最多值,和啟動值。設在邊
明顯地數據範圍極小,可以考慮暴試。設
D: 待補。
訂閱:
意見 (Atom)


