給定N和K,問有多少棵高度為K、N個頂點的二叉樹。對二叉樹的要求是除葉子外所有頂點必須有兩個子節點。
明明是很簡單的動態規劃,卻搞了我很多時間…
定義目標函數 F[N][K] 即題目要求數。
觀察﹕
(1) F[N][K]必須依賴 F[i][K-1],使得二叉樹數符合要求。
(2) 必須分配單數子節點予任意子樹,否則必得無乎合要求的二叉樹。
(3) 得出轉移方程為 F[i][K-1] * F[N-1-i][j] * 2 的總和,當中 j < K-1。
(4) 另需加上F[i][K-1] * F[N-i-1][K-1],因為交換子樹視同相等。
(5) 合法狀態必須符合 2*K < N + 2,因為一棵符合要求的子樹至少是Left Completed,必然有2 * K - 1點,否則無法構建二叉樹。
沒有留意(5)便會造成很多無謂的錯誤。
2009年7月21日 星期二
2009年7月20日 星期一
ICPC 2563 Picture Puzzle
給定九個版塊,每一塊對應四邊的字母的導向(左或右),可以透過旋轉及隨意擺於位置,構造出可行還原情況。可行的意思指若兩個版塊相鄰,它們必須對應相字的字母且導向不相同。除了中間的那塊不可旋轉。求任意可行解。
基本上與數獨解差不多,甚至乎比它要簡單。每次放置版塊的時候要記下它是哪一塊,還有旋轉了多少遍(最多3遍)。假設放置次序依上至下、左至右的順序,則只在放置後檢查左及上方的版塊即成。
撇除輸出格式,本題也是簡單窮舉練習題。

ICPC2559 Number Base Conversion
題目給出  進制的
進制的 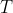 ,把它轉化成
,把它轉化成 進制。
進制。
Java本身就有這種函數,所以C/C++寫會很慘。
基本上按題意做就可以。
我的方法是先吧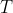 轉化成十進制再轉成
轉化成十進制再轉成 進制。
進制。
至於轉成十進制的方法也並非困難,利用Honor's Rule就可以了。
Honor's Rule大意是用於多項式代數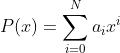
可以基於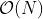 的計算
的計算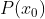 ﹕
﹕
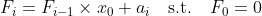
然後寫個好的大數除法及除式便可以了。
注意輸出為0的情況。
Java本身就有這種函數,所以C/C++寫會很慘。
基本上按題意做就可以。
我的方法是先吧
至於轉成十進制的方法也並非困難,利用Honor's Rule就可以了。
Honor's Rule大意是用於多項式代數
可以基於
然後寫個好的大數除法及除式便可以了。
注意輸出為0的情況。
ICPC2556 Four Quarters
題目給出玩者間的得失矩陣,說明兩位玩者各擲錢幣兩次後對應的得失情況,並問第1至20回合間的勝負比率。
這是一道頗簡單的動態規劃題。
假定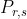 為在第
為在第 回合,玩者
回合,玩者 的得分減去玩者
的得分減去玩者 的得分為
的得分為 的概率。
的概率。
轉移方程便是
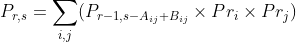
當中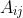 及
及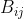 便是兩位玩者的分數,
便是兩位玩者的分數,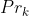 代表發生結果
代表發生結果 的概率。比如
的概率。比如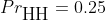 。
。
撇除輸出,這是一道經典的題目。
這是一道頗簡單的動態規劃題。
假定
轉移方程便是
撇除輸出,這是一道經典的題目。
ICPC 2557 The Drunk Jailer
題意說給了N道門,某男會做如下事件N次﹕
在第i次中,把i, 2i, 3i. . . 的門做手腳。如果該門是鎖著的,他會解鎖;否則重新把它鎖上。
問,有多少道門是解鎖?假設一開始所有門都是鎖上的。
由於N少於100,故以簡單的枚舉即可通過。在這裡不妨給大家另一種解題思路。
想想第i道門會被某男遇上多少次呢?答案顯然是i的因數總數。
我們知道當門被遇上偶數次,門最後必然被鎖上。但,問何時才會遇上奇數遍?
若把N寫成a x b,肯定如果在第a會遇上次門,第b次會同樣遇上。
因為如此,除非a = b,否則門必然被訪問偶數遍。
得出結論﹕只有平方數的門才會被某男訪問奇數遍。
問題轉化成﹕給出N,問有多少平方數少於等於N。
輕鬆解決。
在第i次中,把i, 2i, 3i. . . 的門做手腳。如果該門是鎖著的,他會解鎖;否則重新把它鎖上。
問,有多少道門是解鎖?假設一開始所有門都是鎖上的。
由於N少於100,故以簡單的枚舉即可通過。在這裡不妨給大家另一種解題思路。
想想第i道門會被某男遇上多少次呢?答案顯然是i的因數總數。
我們知道當門被遇上偶數次,門最後必然被鎖上。但,問何時才會遇上奇數遍?
若把N寫成a x b,肯定如果在第a會遇上次門,第b次會同樣遇上。
因為如此,除非a = b,否則門必然被訪問偶數遍。
得出結論﹕只有平方數的門才會被某男訪問奇數遍。
問題轉化成﹕給出N,問有多少平方數少於等於N。
輕鬆解決。
2009年7月16日 星期四
PKU 1466 Boys and Girls
想不到這道是若干年後被改難然後翻炒…
題意說給出N人,每人會對某幾個人有關係,問最多可以選多少人,使得這群人互相不會有關係。
如果把沒有關係的人連一條邊,題目正好就是求Maximum Clique。不過這道題給的不是這條邊,而是赤裸裸的告訴你這是二分圖。明顯地求Maximum Independent Set。輕輕用簡單的二分圖匹配就搞定了。
至於難版的那個,只是沒有這般赤裸裸而已…
題意說給出N人,每人會對某幾個人有關係,問最多可以選多少人,使得這群人互相不會有關係。
如果把沒有關係的人連一條邊,題目正好就是求Maximum Clique。不過這道題給的不是這條邊,而是赤裸裸的告訴你這是二分圖。明顯地求Maximum Independent Set。輕輕用簡單的二分圖匹配就搞定了。
至於難版的那個,只是沒有這般赤裸裸而已…
UVa 11504 Dominos
題目大意就是給出 塊骨牌,
塊骨牌, 個關係,每個關係以x y表示「如果骨牌x倒了,骨牌y也會倒下」。
個關係,每個關係以x y表示「如果骨牌x倒了,骨牌y也會倒下」。
問最少要推多少塊骨牌才會讓所有骨牌倒下。
最初蠢蠢的以為只求離散集的個數便成,結果沒留意到x y不代表y x,所以離散集會誤以為兩者關係相等,必然出錯。
細心留意,可以兩個觀察。
(1) 如果存在x使得沒有z x的話,我們必須推x。(Topological Sort即便如此)
(2) 若果有一個群組中每一塊骨牌都可以直接或間接以關係把其餘所有骨牌推下,則只需推其一塊便等於把群組中的每塊骨牌推一下,省力省時。
(2)的對群組的定義便正正是強連通塊(Strongly Connected Components)的詮釋。因為「推一塊便等於推其他塊」的想法下,我們不妨把這個塊縮成一點,並把當中骨牌成員的出入塊的邊保留。結合(1)的想法,毋需做拓撲排序,直接計算入邊為零的點(若未屬任何塊,當然它自己也可以成一塊)或塊即成。
問最少要推多少塊骨牌才會讓所有骨牌倒下。
最初蠢蠢的以為只求離散集的個數便成,結果沒留意到x y不代表y x,所以離散集會誤以為兩者關係相等,必然出錯。
細心留意,可以兩個觀察。
(1) 如果存在x使得沒有z x的話,我們必須推x。(Topological Sort即便如此)
(2) 若果有一個群組中每一塊骨牌都可以直接或間接以關係把其餘所有骨牌推下,則只需推其一塊便等於把群組中的每塊骨牌推一下,省力省時。
(2)的對群組的定義便正正是強連通塊(Strongly Connected Components)的詮釋。因為「推一塊便等於推其他塊」的想法下,我們不妨把這個塊縮成一點,並把當中骨牌成員的出入塊的邊保留。結合(1)的想法,毋需做拓撲排序,直接計算入邊為零的點(若未屬任何塊,當然它自己也可以成一塊)或塊即成。
PKU3680 Intervals
如此這般,開始寫中文。
以後頹題難題只要解了就寫。
先說這道題,大意就是給定一堆Open Intervals,要保証選取某些Intervals使實數軸上的數字不會被覆蓋超過 次,並且把選取的Intervals的獲利總數最大化。
次,並且把選取的Intervals的獲利總數最大化。
好的,看起來很複雜對吧?不難發現用任何DP方法都應該得不到正確的結果。於是我們從題意直接著手。就取Sample最後一例說明吧。
把Intervals(不按比例)畫出來會成這個樣子﹕
1: |-----------------------------------------|
2: |--------------|
3: |---------------|
----------------------------------------------
1 100 150 200 10萬
假設第i區間取次Xi,從Sample我們可得X1, X2, X3。
把Intervals作離散化,可以得到以下4道不等式。同色Intervals代表屬同一不等式。
X1 + X2 <= K .....(1)
X1 + X2 + X3 <= K .....(2)
X1 + X3 <= K ..... (3)
X1 <= K ..... (4)
一般來說處理不等式都不好辦,我們嘗試引入鬆弛量(不是熊) Slack Variables,讓不等試變等式。
X1 + X2 + Y1 = K .....(1)
X1 + X2 + X3 + Y2 = K .....(2)
X1 + X3 + Y3 = K ..... (3)
X1 + Y4 = K ..... (4)
若果讓第i式與第i+1式相減(不包括i = 4),按植樹原理可以得3式﹕
(2) - (1): X3 + Y2 = Y1
(3) - (2): Y3 = X2 + Y2
(4) - (3): Y4 = X3 + Y3
補上(1)及(4),可得以下5式﹕
X1 + X2 + Y1 = K
X3 + Y2 = Y1
Y3 = X2 + Y2
Y4 = X3 + Y3
K = X1 + Y4 (我把這式倒轉了)
你可以發現,左式相加,就是右式,恰好得到了F=F這個結論。 我們再想深一層,如果套用 F_in = F_out,就是網絡流的守衡定律﹗(Flow Conservation) 若左式是代表入流量,右式便正好了是代表出流量。式子間的關係就可以靠變量來連繫了(比如出流式3聯繫了入流式2)。由此我們可以看式子就是點,變數就是 邊。假如變數X在第i式是出流,在第j式是入流,圖裡便有一條邊 i---->j。相通了這相的東西後,你可以利用變數Xi和Yi來構出一張圖。不過你會發現一件事﹕
(1) Constant怎樣處理?
(2) Source和Sink在哪?
想到這裡,你便猜到Constant的出入流正是對應Source和Sink。
好了。圖是出來了。問題是網絡中的Capacity到底是怎樣?
我們可以這樣分類﹕
Xi: 它代表選或不選第i個interval,故此Capacity頂多是1。
Yi: 它是調節不等式的變數,其值有修正不等式作用,故Capacity可取任意 (即無限)。
常數﹕就是Source / Sink的Capacity。
因 為這題不是要我們選最多的Intervals,而是把獲利最大化,我們便要考慮最小費用流(Min Cost Flow)。費用從何而定?當然費用就是選取Xi與否。故代表Xi的費用就是-Ci,基於最小費用流下我們可以得最小的負數費用(最後把它再負一次便 成)。最後構圖如下﹕
顯然易見,費用流得出最小費用為-100301,取絕對值便是答案。
問題來了﹕構圖不易。
留意以下觀察。
(1) 不失一般性,假設第i個interval的超始點必不多於第i+1個。構建式子時,若第P式開始出現變量Xi,Xi最後出現在式子Q,肯定Xi不會無故於P至Q式之間消失。因為Interval是連續嘛…
(2) 利用兩連續式相減,P式子減去P-1式子時必然利剩下Xi在左式(這不用証明吧…)。當Q+1式減Q式時,該式子的右邊必然出現Xi(取同樣道理)。至此 若果完全明白的話,你會明白為何第1式必須留下,原因是第一式首次出現的變數沒有上一式可以減,反而式子本身就有它們在了。而最後一式最倒轉也是基於這個 原理。
(3) 假設有N等式。經此構造會有 N-1 兩兩相減式 + 2 首尾式 = N+1 式。其中如果第i式左邊出現Yi,右式因為相減下令Yi出現在第i+1式的右邊。
由此得知,若Xi出現在式子P至Q之間,肯定得出邊 (Q+1)-->P。亦可以發現Source必須接N+1式,1式必須接Sink。因此無需處理複雜式子間關係才能構圖。
問題又來了﹕如何得知式子數?
這 問題是對離散化不熟悉的人最常見的(我也是)。一般構建方法可以記錄Intervals的Start及End,對應+1或-1然後便知變數屬甚麼範圍的式 子。此方正確但難以處理區間邊緣重疊的問題,容易出錯。我的做法是把所有Intervals的起點終點的**唯一數字**排序,那麼這個數字的次序便對應 起點的出現在甚麼式子的左邊,和終結時變數應該會在甚麼式子的右式出現。再以Sample為例,可以如下數字﹕
次序 | 1 2 3 4 5
數字 | 1 100 150 200 100000
取第二Interval為例,X2出現在第1式的左邊和第3式的右邊,故此得出3-->1的邊。
知道這個便是貼模版的時候。你會發覺不對勁﹕負邊用Bellman-Ford會否出現Negative Cycle?答案是否定的。Negative Cycle不會出現在這種構圖中,你可以再慢慢証明。然而當你放心貼上Bellman-Ford的時候,會發現PKU上會說TLE…因此,你可以嘗試用用 SPFA(Shortest Path Faster Algorithm)。然後,又是超時。原因是,SPFA對層圖處理比較慢,所以要加上優化。只要加上SLF(Shortest Label First)即可以極速AC。再加上LLL(Largest Label Last)只是錦上添花,想嘗試寫寫亦無傷大雅。
以後頹題難題只要解了就寫。
先說這道題,大意就是給定一堆Open Intervals,要保証選取某些Intervals使實數軸上的數字不會被覆蓋超過
好的,看起來很複雜對吧?不難發現用任何DP方法都應該得不到正確的結果。於是我們從題意直接著手。就取Sample最後一例說明吧。
把Intervals(不按比例)畫出來會成這個樣子﹕
1: |-----------------------------------------|
2: |--------------|
3: |---------------|
----------------------------------------------
1 100 150 200 10萬
假設第i區間取次Xi,從Sample我們可得X1, X2, X3。
把Intervals作離散化,可以得到以下4道不等式。同色Intervals代表屬同一不等式。
X1 + X2 <= K .....(1)
X1 + X2 + X3 <= K .....(2)
X1 + X3 <= K ..... (3)
X1 <= K ..... (4)
一般來說處理不等式都不好辦,我們嘗試引入鬆弛量(不是熊) Slack Variables,讓不等試變等式。
X1 + X2 + Y1 = K .....(1)
X1 + X2 + X3 + Y2 = K .....(2)
X1 + X3 + Y3 = K ..... (3)
X1 + Y4 = K ..... (4)
若果讓第i式與第i+1式相減(不包括i = 4),按植樹原理可以得3式﹕
(2) - (1): X3 + Y2 = Y1
(3) - (2): Y3 = X2 + Y2
(4) - (3): Y4 = X3 + Y3
補上(1)及(4),可得以下5式﹕
X1 + X2 + Y1 = K
X3 + Y2 = Y1
Y3 = X2 + Y2
Y4 = X3 + Y3
K = X1 + Y4 (我把這式倒轉了)
你可以發現,左式相加,就是右式,恰好得到了F=F這個結論。 我們再想深一層,如果套用 F_in = F_out,就是網絡流的守衡定律﹗(Flow Conservation) 若左式是代表入流量,右式便正好了是代表出流量。式子間的關係就可以靠變量來連繫了(比如出流式3聯繫了入流式2)。由此我們可以看式子就是點,變數就是 邊。假如變數X在第i式是出流,在第j式是入流,圖裡便有一條邊 i---->j。相通了這相的東西後,你可以利用變數Xi和Yi來構出一張圖。不過你會發現一件事﹕
(1) Constant怎樣處理?
(2) Source和Sink在哪?
想到這裡,你便猜到Constant的出入流正是對應Source和Sink。
好了。圖是出來了。問題是網絡中的Capacity到底是怎樣?
我們可以這樣分類﹕
Xi: 它代表選或不選第i個interval,故此Capacity頂多是1。
Yi: 它是調節不等式的變數,其值有修正不等式作用,故Capacity可取任意 (即無限)。
常數﹕就是Source / Sink的Capacity。
因 為這題不是要我們選最多的Intervals,而是把獲利最大化,我們便要考慮最小費用流(Min Cost Flow)。費用從何而定?當然費用就是選取Xi與否。故代表Xi的費用就是-Ci,基於最小費用流下我們可以得最小的負數費用(最後把它再負一次便 成)。最後構圖如下﹕
問題來了﹕構圖不易。
留意以下觀察。
(1) 不失一般性,假設第i個interval的超始點必不多於第i+1個。構建式子時,若第P式開始出現變量Xi,Xi最後出現在式子Q,肯定Xi不會無故於P至Q式之間消失。因為Interval是連續嘛…
(2) 利用兩連續式相減,P式子減去P-1式子時必然利剩下Xi在左式(這不用証明吧…)。當Q+1式減Q式時,該式子的右邊必然出現Xi(取同樣道理)。至此 若果完全明白的話,你會明白為何第1式必須留下,原因是第一式首次出現的變數沒有上一式可以減,反而式子本身就有它們在了。而最後一式最倒轉也是基於這個 原理。
(3) 假設有N等式。經此構造會有 N-1 兩兩相減式 + 2 首尾式 = N+1 式。其中如果第i式左邊出現Yi,右式因為相減下令Yi出現在第i+1式的右邊。
由此得知,若Xi出現在式子P至Q之間,肯定得出邊 (Q+1)-->P。亦可以發現Source必須接N+1式,1式必須接Sink。因此無需處理複雜式子間關係才能構圖。
問題又來了﹕如何得知式子數?
這 問題是對離散化不熟悉的人最常見的(我也是)。一般構建方法可以記錄Intervals的Start及End,對應+1或-1然後便知變數屬甚麼範圍的式 子。此方正確但難以處理區間邊緣重疊的問題,容易出錯。我的做法是把所有Intervals的起點終點的**唯一數字**排序,那麼這個數字的次序便對應 起點的出現在甚麼式子的左邊,和終結時變數應該會在甚麼式子的右式出現。再以Sample為例,可以如下數字﹕
次序 | 1 2 3 4 5
數字 | 1 100 150 200 100000
取第二Interval為例,X2出現在第1式的左邊和第3式的右邊,故此得出3-->1的邊。
知道這個便是貼模版的時候。你會發覺不對勁﹕負邊用Bellman-Ford會否出現Negative Cycle?答案是否定的。Negative Cycle不會出現在這種構圖中,你可以再慢慢証明。然而當你放心貼上Bellman-Ford的時候,會發現PKU上會說TLE…因此,你可以嘗試用用 SPFA(Shortest Path Faster Algorithm)。然後,又是超時。原因是,SPFA對層圖處理比較慢,所以要加上優化。只要加上SLF(Shortest Label First)即可以極速AC。再加上LLL(Largest Label Last)只是錦上添花,想嘗試寫寫亦無傷大雅。
訂閱:
意見 (Atom)


