PKU 2046 Gap

This is a question from Japan Regional Contest 2003

Given 4x8 grid map, which is filled with 28 distinct numbers on the right 4x7 grids, ranging from 11-17, 21-27, 31-37 and 41-47. The left 4x1 grids are left as spaces. Then swap the spaces with 11, 21, 31 and 41 such that the left 4x1 grids are from top 11, 21, 31 and to bottom 41, respectively. The game then starts. Each time the spaces can swap with the next numbers from its left, e.g. 47 can be swapped with a space whose left grid contains 46. Note that under this rule, any space cannot perform swapping if its left is either 17, 27, 37 and 47. The game ends when the map is as follow:

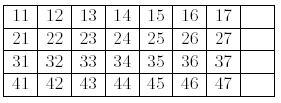
The question asks the minimum step to achieve the goal, given the initial state.

Clearly, the sample input gives the worst case of 60 steps, so you can think that the possible and reachable states should be much less than . Applying BFS should be plausible. Since the state representation in integer is difficult, one may choose the hash the state with slight conflict. Then store the state using hash table. Under sufficiently good hashing function and small hash size, the program can pass the time limit. Note that, since the steps and grid map stores small integer, using short when declaring the structure is always preferred.

The hash function I choose is

Hash table size is 66271

PKU3410 Split Convex Polygon

This is a problem from Northeastern Europe Western Subregion 2002.

The problem asks if two polygons and are originally from splitting a convex polygon, by only translations and rotations. The points are given in anticlockwise order.

The general idea is that we enumerate all edges pair and see if have the same length. Then we can say that they are suitable for overlapping. This is the very first condition for and to be combined since if they have different length and combined, a concave angle is always generated. Then we continue to find how many edges next to has same length to those previous to , plus the condition that their angles turned must be the same. As we tracing backward is more complicated, we may consider the invert ordering of one polygon.
The next thing we are going to check is that the angle made by and it's previous edge and the angle made by and it's previous edge. The objective is to check whether this endpoint would combine to a convex vertex (i.e. ). Same thing goes to the last matched point.
Lastly we should check the unmatched edges of both polygon and see if those edges are convex or not.

Sample test data:


One of the extreme cases:

PKU1092 - Farmland

This problem is from Korea Taejon regional 2001.

The general idea to this question is about:

Given a graph , you are asked to count how many polygons that satisfy the following properties:

1. It is a sided polygon
2. The area is positive
3. The polygon should not contains any vertex and edge inside (except the boundaries)

The idea is to enumerate all edges and to traverse if there exists a complete polygon-cycle.
The way to traverse is shown below:

1. Suppose we have a vector as a first to-be-traversed vector
2. Find a vector such that , and the anti-clockwise angle turned from to , is maximized. How to determine? We can try the following method:
   
   • Let the inclined angle made by be .
   • Let function
   • Let a transformation is to rotate radian clockwise
     
   • 
     
3. Then maximize
4. Replace by
   
5. Each time we log down how many times we have visited. If we have seen that is visited 3 times, then we can stop traversing.
6. If we have maintained a traversal list, check if the content is 2-repeated e.g. ABCDABCD
7. If is 2-repeated, has required length and anticlockwise in representation, we can conclude that it is a valid polygon that satisfies the constraints

Suppose we found a polygon-cycle ABCD, we know that there exists 4 different valid permutations, namely ABCD, BCDA, CDAB and DABC. It can be proved by the cycle properties possessed of the polygon-chain. Then, we can conclude that if we have found valid polygon-cycles, the actual answer would be since we can find all those permutations.

Struggled Testcase: